题目内容
15.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的取值范围为k≤4.分析 分为两种情况:①当k-3≠0时,(k-3)x2+2x+1=0,求出△=b2-4ac=-4k+16≥0的解集即可;②当k-3=0时,得到一次函数y=2x+1,与X轴有交点;即可得到答案.
解答 解:①当k-3≠0时,(k-3)x2+2x+1=0,
△=b2-4ac=22-4(k-3)×1=-4k+16≥0,
k≤4;
②当k-3=0时,y=2x+1,与x轴有交点;
故k的取值范围是k≤4,
故答案为:k≤4.
点评 本题主要考查对抛物线与x轴的交点,根的判别式,一次函数的性质等知识点的理解和掌握,能进行分类求出每种情况的k是解此题的关键.

练习册系列答案
相关题目
5.设a1,a2,…,a10是从1,0,-1这三个数中取值的一列数,若a1+a2+…+a10=1,(a1+1)2+(a2+1)2+…+(a10+1)2=17,则a1,a2,…,a10中1的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
10.若x<-5,则下列不等式成立的是( )
| A. | x2>-5x | B. | x2≥-5x | C. | x2<-5x | D. | x2≤-5x |
6.已知a,b,c均为实数,且a>b,c≠0,则下列结论不一定正确的是( )
| A. | a+c>b+c | B. | -a<-b | C. | a2>b2 | D. | $\frac{a}{{c}^{2}}$>$\frac{b}{{c}^{2}}$ |
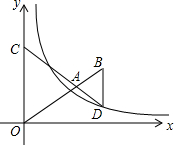 如图,△ACO和△ABD都是等边三角形,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点D,若OA2-AB2=8$\sqrt{3}$,则k的值为( )
如图,△ACO和△ABD都是等边三角形,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点D,若OA2-AB2=8$\sqrt{3}$,则k的值为( )