题目内容
2.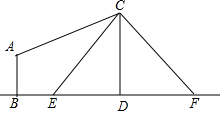 如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=$\sqrt{3}$米,BE=3米,求拉线CE的长.
如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=$\sqrt{3}$米,BE=3米,求拉线CE的长.
分析 过A作AM垂直于CD,垂足为M,根据正切的定义出去CM,得到DE的长,根据勾股定理计算即可.
解答 解:过A作AM垂直于CD,垂足为M,
则AM=BD=6,
∴CM=AM×tan∠ACM=2$\sqrt{3}$,
∴CD=CM+MD=3$\sqrt{3}$,又DE=3
利用勾股定理得CE=$\sqrt{C{D}^{2}+D{E}^{2}}$=6米
答:拉线CE的长6米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
10.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 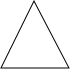 等边三角形 | B. |  平行四边形 | C. |  正六边形 | D. |  五角星 |
7.“关于x的函数y=(1-m)x2+2x+1的图象与x轴至少有一个交点”是真命题,则m的值不可以是( )
| A. | m=1 | B. | m=0 | C. | m=-1 | D. | m=2 |
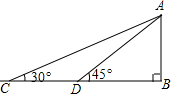 如图,某数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端点A的仰角为30°,再向旗杆的方向前进12米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端点A的仰角为45°,请计算旗杆AB的高度.(结果保留根号)
如图,某数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端点A的仰角为30°,再向旗杆的方向前进12米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端点A的仰角为45°,请计算旗杆AB的高度.(结果保留根号)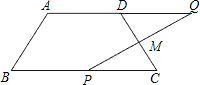 如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.
如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.
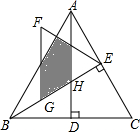 如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{\sqrt{3}}{6}$.
如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{\sqrt{3}}{6}$.