题目内容

13．如果实数x、y，满足|x+2|+（x+y）2=0，那么xy的值等于（　　）
A．-$\frac{1}{4}$B．$\frac{1}{4}$C．-4D．4

分析 根据非负数的和为零，可得每个非负数同时为零，可得x、y的值，根据负数的偶数次幂是正数，可得答案．

解答 解：由|x+2|+（x+y）2=0，得
x+2=0，y+x=0．
解得x=-2，y=2．
那么xy的值等于4，
故选：D．

点评 本题考查了非负数的性质，利用非负数的和为零得出每个非负数同时为零是解题关键．

练习册系列答案
相关题目
6．某超市为了促销，准备开展限时摸奖活动，规定每晚7：00～7：15之间购物的前10位（假定此段时间购物人数不少于10人）顾客，每人可以享受一次摸奖机会．奖项分别设为一、二、三等奖，其中一等奖1名，二等奖2名，三等奖3名．请回答下列问题：
（1）某位参与摸奖顾客恰好摸到三等奖的概率是$\frac{3}{10}$；
（2）试用树状图或表格进行说明，如果在获奖的顾客当中任意抽出两位，恰好都是二等奖的概率是多少？
（3）若以卡片作为替代物进行以上摸奖模拟实验，一个同学提供了部分实验操作：①准备10张除标记不同，大小形状均相同的卡片；②把卡片按1：2：3的比例涂成三种颜色；③让用于实验的卡片有且只有1个为一等奖标记、有且只有2个为二等奖标记、有且只有3个为三等奖标记．你认为其中操作正确的序号是①③．
7．不解方程，判断下列方程根的情况．
（1）y2-3y-1=0；
（2）3x2-2x+1=0；
（3）x2-2$\sqrt{3}$x+3=0．
1．如图，平面直角坐标系xOy中，一次函数y=-x+b（b为常数，b＞0）的图象与x轴、y轴分别相交于点A、B，半径为1的⊙O与x轴正半轴相交于点C，与y轴正半轴相交于点D．
（1）如图1，点E是⊙O上的动点（与点C、D不重合），则∠DEC=45°或135°°．
（2）当b=$\sqrt{2}$时，直线AB与⊙O相切；当b满足b＞$\sqrt{2}$时，直线AB与⊙O相离；
（3）如图2，点E是⊙O上的动点，过点E作⊙O的切线交直线AB于点P，连接PO，当b=4时，求PE长的最小值．
8．已知|a-b-$\sqrt{17}$|+$\sqrt{ab-2}$=0
（1）求（a-1）（b+1）的值．
（2）求a2+b2的值．
（3）求ab3-a3b的值．
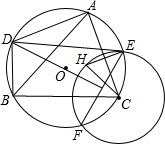18．如图，H为△ABC的垂心，圆O为△ABC的外接圆．点E、F为以C为圆心、CH长为半径的圆与圆O的交点，D为线段EF的垂直平分线与圆O的交点．求证：
（1）AC垂直平分线段HE；
（2）DE=AB．
5．若a，b为实数，且|a+$\frac{1}{3}$|+$\sqrt{b-3}$=0，则（ab）2016的值是（　　）
A．0B．1C．-1D．±1
2．如图，在平面直角坐标系中，A（10，0），以OA为直径在第一象限内作半圆，B为半圆上一点，连接AB并延长至C，使BC=AB，过C作CD⊥x轴于点D，交线段OB于点E．已知CD=8，抛物线经过O，E，A三点．
（1）求直线OB的函数表达式；
（2）求抛物线的函数表达式；
（3）若P为抛物线上位于第一象限内的一个动点，以P，O，A，E为顶点的四边形面积记作S，则S取何值时，相应的点P有且只有3个．
3．如图为某物体简化的主视图和俯视图，猜想该物体可能是（　　）
A．光盘B．双层蛋糕C．游泳圈D．铅笔

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网