题目内容
8.已知|a-b-$\sqrt{17}$|+$\sqrt{ab-2}$=0(1)求(a-1)(b+1)的值.
(2)求a2+b2的值.
(3)求ab3-a3b的值.
分析 根据首先根据任何数的平方、绝对值都是非负数,两个非负数的和是0,则每个非负数等于0,据此即可求的a和b的值.
(1)首先利用多项式的乘法法则计算,然后把(1)中的结果代入求解;
(2)根据a2+b2=(a-b)2+2ab,直接代入即可求解;
(3)首先求得a和b的值,然后代入求解.
解答 解:根据题意得:$\left\{\begin{array}{l}{a-b-\sqrt{17}=0}\\{ab-2=0}\end{array}\right.$,
则a-b=$\sqrt{17}$,ab=2.
(1)原式=ab+(a-b)-1=2+$\sqrt{17}$-1=1+$\sqrt{17}$;
(2)原式=(a-b)2+2ab=($\sqrt{17}$)2+2×2=17+4=21;
(3)根据题意得:$\left\{\begin{array}{l}{a-b=\sqrt{17}}\\{ab=2}\end{array}\right.$,
则a+b=±$\sqrt{(a-b)^{2}+4ab}$=±$\sqrt{(\sqrt{17})^{2}+4×2}$=±5.
则原式=ab(a+b)(a-b)=2×(±5)×$\sqrt{17}$=±10$\sqrt{17}$.
点评 本题考查了非负数的性质,两个非负数的和是0,则每个非负数等于0,初中范围内的非负数有:任何数的偶次方、算术平方根以及绝对值.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
19.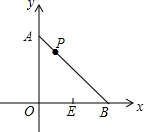 如图,在平面直角坐标系中,A、B两点的坐标分别为(0,2),(2,0),E为OB的中点,P是线段AB上的一个动点,则PE+PO的最小值为( )
如图,在平面直角坐标系中,A、B两点的坐标分别为(0,2),(2,0),E为OB的中点,P是线段AB上的一个动点,则PE+PO的最小值为( )
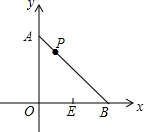 如图,在平面直角坐标系中,A、B两点的坐标分别为(0,2),(2,0),E为OB的中点,P是线段AB上的一个动点,则PE+PO的最小值为( )
如图,在平面直角坐标系中,A、B两点的坐标分别为(0,2),(2,0),E为OB的中点,P是线段AB上的一个动点,则PE+PO的最小值为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
13.如果实数x、y,满足|x+2|+(x+y)2=0,那么xy的值等于( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -4 | D. | 4 |
18.等腰三角形三边长分别为a、b、4,且a、b是关于x的一元二次方程x2-12x+k+2=0的两根,则k的值为( )
| A. | 30 | B. | 34或30 | C. | 36或30 | D. | 34 |
