题目内容
1.如图,平面直角坐标系xOy中,一次函数y=-x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为1的⊙O与x轴正半轴相交于点C,与y轴正半轴相交于点D.(1)如图1,点E是⊙O上的动点(与点C、D不重合),则∠DEC=45°或135°°.
(2)当b=$\sqrt{2}$时,直线AB与⊙O相切;当b满足b>$\sqrt{2}$时,直线AB与⊙O相离;
(3)如图2,点E是⊙O上的动点,过点E作⊙O的切线交直线AB于点P,连接PO,当b=4时,求PE长的最小值.

分析 (1)只需分点E在优弧和劣弧上两种情况讨论,然后运用圆周角定理和圆内接四边形的对角互补就可解决问题;
(2)过点O作OH⊥AB于H,如图1,运用面积法求出OH,然后根据OH=r时直线与圆相切及OH>r时直线与圆相离就可解决问题;
(3)连接OE,如图2,根据圆的切线的性质可得∠OEP=90°,根据勾股定理可得EP=$\sqrt{O{P}^{2}-O{E}^{2}}$=$\sqrt{O{P}^{2}-1}$.要求EP的最小值,只需OP最小,只需求出OP⊥AB时OP的值,就可解决问题.
解答 解:(1)当点E在优弧上时,∠CED=$\frac{1}{2}$∠COD=45°;
当点E在劣弧上时,∠CED=180°-45°=135°.
故答案为45°或135°.
(2)过点O作OH⊥AB于H,如图1.
∵点A、B是直线y=-x+b与x轴、y轴的交点,
∴A(b,0),B(0,b).
∵b>0,
∴OA=OB=b,
∴AB=$\sqrt{2}$b.
∵S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•OH,
∴OH=$\frac{OA•OB}{AB}$=$\frac{{b}^{2}}{\sqrt{2}b}$=$\frac{b}{\sqrt{2}}$.
当OH=1即=$\frac{b}{\sqrt{2}}$=1也即b=$\sqrt{2}$时,直线AB与⊙O相切;
当OH>1即$\frac{b}{\sqrt{2}}$>1也即b>$\sqrt{2}$时,直线AB与⊙O相离.
故答案为:$\sqrt{2}$,b>$\sqrt{2}$;
(3)连接OE,如图2.
∵PE与⊙O相切于E,
∴∠OEP=90°,
∴EP=$\sqrt{O{P}^{2}-O{E}^{2}}$=$\sqrt{O{P}^{2}-1}$.
当OP⊥AB时,OP取到最小值,最小值为$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$,
此时EP最小,最小值为$\sqrt{(2\sqrt{2})^{2}-1}$=$\sqrt{7}$,
∴PE长的最小值为$\sqrt{7}$.
点评 本题主要考查了直线与圆的位置关系、圆的切线的性质、勾股定理、圆周角定理、圆内接四边形的对角互补等知识,把求EP的最小值转化为求OP的最小值,是解决第(3)小题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 3 | B. | 4 | C. | 3或5 | D. | 3或4 |
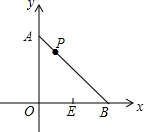 如图,在平面直角坐标系中,A、B两点的坐标分别为(0,2),(2,0),E为OB的中点,P是线段AB上的一个动点,则PE+PO的最小值为( )
如图,在平面直角坐标系中,A、B两点的坐标分别为(0,2),(2,0),E为OB的中点,P是线段AB上的一个动点,则PE+PO的最小值为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -4 | D. | 4 |
 如图,扇形OAB是圆锥的侧面展开图,且点O、A、B分别是格点,已知小正方形方格的边长为1cm,则这个圆锥的底面半径为$\frac{\sqrt{2}}{2}$cm.
如图,扇形OAB是圆锥的侧面展开图,且点O、A、B分别是格点,已知小正方形方格的边长为1cm,则这个圆锥的底面半径为$\frac{\sqrt{2}}{2}$cm.