Question

18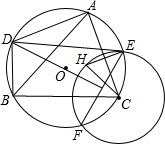．如图，H为△ABC的垂心，圆O为△ABC的外接圆．点E、F为以C为圆心、CH长为半径的圆与圆O的交点，D为线段EF的垂直平分线与圆O的交点．求证：
（1）AC垂直平分线段HE；
（2）DE=AB．

Answer 1

分析 （1）如图根据三角形垂心的性质得到∠AHC+∠ABC=180°，由圆内接四边形的性质得到∠AEC+∠ABC=180°，等量代换得到∠AEC=∠AHC，于是得到AE=AH，即可得到结论；
（2）由D为线段EF的垂直平分线与圆O的交点，推出CD为圆O的直径，根据圆周角定理得到DA⊥AC，推出B、H、E三点共线，证得$\widehat{DAE}=\widehat{ADB}$，根据圆的性质即可得到结论．

解答 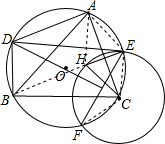证明：（1）如图，连结AH，AE，EC，
由H为△ABC的垂心知，∠AHC+∠ABC=180°，
由A、B、C、E四点共圆，得∠AEC+∠ABC=180°，
∴∠AEC=∠AHC，
∵CH=CE，
∴∠CEH=∠CHE，
∴∠AEH=∠AHE，AE=AH，
∴AC垂直平分线段HE；

（2）连结CF，BH，
∵CE=CH=CF，
∵D为线段EF的垂直平分线与圆O的交点，
∴CD为圆O的直径，
∴DA⊥AC，
∵H为△ABC的垂心知，HE⊥AC，BH⊥AC，
∴B、H、E三点共线，
∴BE⊥AC，
∴∠DCE=90°-∠CDE=90°-∠CBE=∠ACB，
∴$\widehat{DAE}=\widehat{ADB}$，
∴DE=AB．

点评 本题考查了等腰三角形的性质，圆周角定理，三点共线，线段垂直平分线的判定和性质，三角形的垂心的性质，圆内接四边形的性质，利用三角形垂心的性质得到B、H、E三点共线是解题的关键．