��Ŀ����
2�� ��ͼ����ƽ��ֱ������ϵ�У�A��10��0������OAΪֱ���ڵ�һ����������Բ��BΪ��Բ��һ�㣬����AB���ӳ���C��ʹBC=AB����C��CD��x���ڵ�D�����߶�OB�ڵ�E����֪CD=8�������߾���O��E��A���㣮
��ͼ����ƽ��ֱ������ϵ�У�A��10��0������OAΪֱ���ڵ�һ����������Բ��BΪ��Բ��һ�㣬����AB���ӳ���C��ʹBC=AB����C��CD��x���ڵ�D�����߶�OB�ڵ�E����֪CD=8�������߾���O��E��A���㣮��1����ֱ��OB�ĺ�������ʽ��
��2���������ߵĺ�������ʽ��
��3����PΪ��������λ�ڵ�һ�����ڵ�һ�����㣬��P��O��A��EΪ������ı����������S����Sȡ��ֵʱ����Ӧ�ĵ�P����ֻ��3����
���� ��1������Բ�ܽǶ�����ֱ�����Ե�Բ�ܽǵ���90�㣬���ǵõ�OB�ǵĴ�ֱƽ���ߣ���õ�B�����ɵõ�OB����ֱ�ߵĽ���ʽ��
��2����OB����ֱ�ߵĽ���ʽ�ó���E�����꣬�ô���ϵ�����������ߵĽ���ʽ��
��3�����ã�2���Ľ����õ�P�����꣬�������ۣ�������P��CD����࣬�ӳ�OP��CD��Q������ͼ2����OP����ֱ�ߵĺ�����ϵʽ����ʾ��Q��������꣬��QE�ij�����ʾ���ı���POAE�������������P��CD���Ҳ࣬�ӳ�AP��CD��Q������ͼ3����AP����ֱ�ߵĽ���ʽ���Ӷ����Q��������꣬��QE����ı���POAE���������P��CD�Ҳ�ʱ���ı���POAE��������ֵΪ16����ʱ��P��λ�þ�һ������-$\frac{3}{8}$p2+$\frac{9}{4}$p+15=16�����p���ó����ۣ�
��� 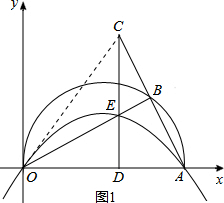 �⣺��1������OC����ͼ1��ʾ��
�⣺��1������OC����ͼ1��ʾ��
��OA�ǡ�O��ֱ����
���OBA=90�㣬
��OB��AC��
�֡�AB=BC��
��OB��AC�Ĵ�ֱƽ���ߣ�
��OC=OA=10��
��Rt��OCD��OC=10��CD=8��
��OD=6��
��C��6��8����B��8��4��
��OB����ֱ�ߵĺ�����ϵΪy=$\frac{1}{2}$x��
��2����E��ĺ�����Ϊ6��
��E��������Ϊ3��
��E��6��3����
�����߹�O��0��0����E��6��3����A��10��0����
����������ߵĺ�����ϵʽΪy=ax��x-10������E���������ã�
3=6a��6-10����
���a=-$\frac{1}{8}$��
��������ߵĺ�����ϵʽΪy=-$\frac{1}{8}$x��x-10������y=-$\frac{1}{8}$x2+$\frac{5}{4}$x��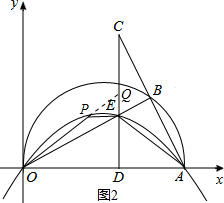 ��3�����P��p��-$\frac{1}{8}$p2+$\frac{5}{4}$p����
��3�����P��p��-$\frac{1}{8}$p2+$\frac{5}{4}$p����
������P��CD����࣬�ӳ�OP��CD��Q������ͼ2��
OP����ֱ�ߺ�����ϵʽΪ��y=��-$\frac{1}{8}$p+$\frac{5}{4}$��x
�൱x=6ʱ��y=-$\frac{3}{4}$p+$\frac{15}{2}$����Q��������Ϊ-$\frac{3}{4}$p+$\frac{15}{2}$��
��QE=-$\frac{3}{4}$p+$\frac{15}{2}$-3=-$\frac{3}{4}$p+$\frac{9}{2}$��
S�ı���POAE
=S��OAE+S��OPE
=S��OAE+S��OQE-S��PQE
=$\frac{1}{2}$•OA•DE+$\frac{1}{2}$QE•OD-$\frac{1}{2}$•QE•Px•
=$\frac{1}{2}$��10��3+$\frac{1}{2}$����-$\frac{3}{4}$p+$\frac{9}{2}$����6-$\frac{1}{2}$•��-$\frac{3}{4}$p+$\frac{9}{2}$��•��6-p����
=-$\frac{3}{8}$p2+$\frac{9}{4}$p+15��
������P��CD���Ҳ࣬�ӳ�AP��CD��Q������ͼ3��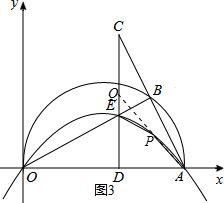
P��p��-$\frac{1}{8}$p2+$\frac{5}{4}$p����A��10��0��
����AP����ֱ�߷���Ϊ��y=kx+b����P��A�������ã�
$\left\{\begin{array}{l}{10k+b=0}\\{pk+b=-\frac{1}{8}{p}^{2}+\frac{5}{4}p}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{1}{8}p}\\{b=\frac{5}{4}p}\end{array}\right.$��
��AP����ֱ�߷���Ϊ��y=$\frac{1}{8}$x+$\frac{5}{4}$��
�൱x=6ʱ��y=$\frac{1}{8}$•6+$\frac{5}{4}$=$\frac{1}{2}$P����Q��������Ϊ$\frac{1}{2}$P��
��QE=$\frac{1}{2}$P-3��
��S�ı���POAE
=S��OAE+S��APE
=S��OAE+S��AQE-S��PQE
=$\frac{1}{2}$•OA•DE+$\frac{1}{2}$•QE•DA-$\frac{1}{2}$•QE•��Px-6��
=$\frac{1}{2}$��10��3+$\frac{1}{2}$•QE•��DA-Px+6��
=15+$\frac{1}{2}$•��$\frac{1}{2}$p-3��•��10-p��
=$\frac{1}{4}$p2+4p
=-$\frac{1}{4}$��p-8��2+16��
�൱P��CD�Ҳ�ʱ���ı���POAE��������ֵΪ16����ʱ��P��λ�þ�һ����
��-$\frac{3}{8}$p2+$\frac{9}{4}$p+15=16����ã�p=3��$\frac{\sqrt{57}}{3}$��
�൱P��CD���ʱ���ı���POAE���������16�Ķ�ӦP��λ����������
������֪����P��O��A��EΪ������ı������S����16ʱ����Ӧ�ĵ�P����ֻ��3����
���� ������Ҫ������Բ�ܽǶ���������ϵ������һ�κ����Ͷ��κ����Ľ���ʽ���ı��κ������ε�����ļ��㣬�����������ؼ������ڽ���������ת��Ϊ�������⣬Ȼ�����ν�Ͻ�����⣮

| A�� | 3 | B�� | 4 | C�� | 3��5 | D�� | 3��4 |
| A�� | -$\frac{1}{4}$ | B�� | $\frac{1}{4}$ | C�� | -4 | D�� | 4 |

 ��ͼ����֪A��-4��$\frac{1}{2}$����B��n��2����һ�κ���y=kx+b�뷴��������y=$\frac{m}{x}$��m��0��ͼ����������㣬AC��x����C��BD��y����D��
��ͼ����֪A��-4��$\frac{1}{2}$����B��n��2����һ�κ���y=kx+b�뷴��������y=$\frac{m}{x}$��m��0��ͼ����������㣬AC��x����C��BD��y����D��