题目内容
15. 有这样一个问题:探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质.小文根据学习函数的经验,对函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质进行了探究.
下面是小文的探究过程,请补充完整:
(1)函数y=$\frac{{x}^{2}}{2x-2}$的自变量x的取值范围是x≠1;
(2)表是y与x的几组对应值.
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{7}{10}$ | $\frac{13}{10}$ | $\frac{3}{2}$ | 2 | 3 | 4 | … |
| y | … | -$\frac{9}{8}$ | -$\frac{2}{3}$ | -$\frac{1}{4}$ | 0 | -$\frac{1}{4}$ | -$\frac{49}{60}$ | $\frac{169}{60}$ | $\frac{9}{4}$ | 2 | m | $\frac{8}{3}$ | … |
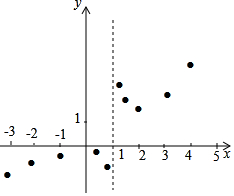
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的性质(一条即可):图象有两个分支,关于点(1,1)中心对称.
分析 (1)由分式有意义的条件可求得答案;
(2)把x=3代入函数解析式可求得答案;
(3)利用描点法可画出函数图象;
(4)结合函数图象可得出答案.
解答 解:
(1)由题意可知2x-2≠0,解得x≠1,
故答案为:x≠1;
(2)当x=3时,m=$\frac{{3}^{2}}{2×3-2}$=$\frac{9}{4}$,
故答案为:$\frac{9}{4}$;
(3)利用描点法可画出函数图象,如图:
(4)由函数图象可知:图象有两个分支,关于点(1,1)中心对称,
故答案为:图象有两个分支,关于点(1,1)中心对称.
点评 本题主要考查函数的性质,掌握自变量的取值范围的求法、描点法画函数图象等是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
6. 如图,在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则BC的长度为( )
如图,在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则BC的长度为( )
 如图,在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则BC的长度为( )
如图,在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则BC的长度为( )| A. | 2 | B. | 8 | C. | $4\sqrt{3}$ | D. | $4\sqrt{5}$ |
10.一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如表:
(1)求这个二次函数的表达式;
(2)求m的值.
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -$\frac{7}{2}$ | 0 | $\frac{5}{2}$ | 4 | $\frac{9}{2}$ | 4 | m | 0 | … |
(2)求m的值.
20.计算$\sqrt{32}$÷$\sqrt{2}$×$\sqrt{3}$的结果估计在( )
| A. | 5至6之间 | B. | 6至7之间 | C. | 7至8之间 | D. | 8至9之间 |