题目内容
10.一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如表:| x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -$\frac{7}{2}$ | 0 | $\frac{5}{2}$ | 4 | $\frac{9}{2}$ | 4 | m | 0 | … |
(2)求m的值.
分析 (1)待定系数法求解可得;
(2)将x=1代入解析式求得y的值,即可得答案.
解答 解:(1)设这个二次函数的表达式为y=a(x-h)2+k.
依题意可知,顶点(-1,$\frac{9}{2}$),
∴$y=a{(x+1)^2}+\frac{9}{2}$.
∵(0,4),
∴$4=a{(0+1)^2}+\frac{9}{2}$.
∴$a=-\frac{1}{2}$.
∴这个二次函数的表达式为$y=-\frac{1}{2}{(x+1)^2}+\frac{9}{2}$.
(2)当x=1时,y=-$\frac{1}{2}$×4+$\frac{9}{2}$=$\frac{5}{2}$,
即$m=\frac{5}{2}$.
点评 本题主要考查待定系数法求函数的解析式,在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
1.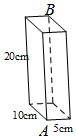 如图,长方体的长为10cm,宽为5cm,高为20cm.若一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路径是( )
如图,长方体的长为10cm,宽为5cm,高为20cm.若一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路径是( )
 如图,长方体的长为10cm,宽为5cm,高为20cm.若一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路径是( )
如图,长方体的长为10cm,宽为5cm,高为20cm.若一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路径是( )| A. | 20+5$\sqrt{5}$ | B. | 25 | C. | 10$\sqrt{5}$+5 | D. | $5\sqrt{21}$ |
18.直四棱柱、长方体和正方体之间的包含关系是( )
| A. |  | B. |  | C. |  | D. |  |
15.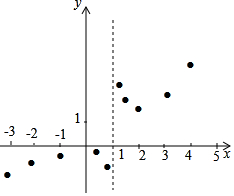 有这样一个问题:探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质.
小文根据学习函数的经验,对函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质进行了探究.
下面是小文的探究过程,请补充完整:
(1)函数y=$\frac{{x}^{2}}{2x-2}$的自变量x的取值范围是x≠1;
(2)表是y与x的几组对应值.
则m的值为$\frac{9}{4}$;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的性质(一条即可):图象有两个分支,关于点(1,1)中心对称.
 有这样一个问题:探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质.小文根据学习函数的经验,对函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质进行了探究.
下面是小文的探究过程,请补充完整:
(1)函数y=$\frac{{x}^{2}}{2x-2}$的自变量x的取值范围是x≠1;
(2)表是y与x的几组对应值.
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{7}{10}$ | $\frac{13}{10}$ | $\frac{3}{2}$ | 2 | 3 | 4 | … |
| y | … | -$\frac{9}{8}$ | -$\frac{2}{3}$ | -$\frac{1}{4}$ | 0 | -$\frac{1}{4}$ | -$\frac{49}{60}$ | $\frac{169}{60}$ | $\frac{9}{4}$ | 2 | m | $\frac{8}{3}$ | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的性质(一条即可):图象有两个分支,关于点(1,1)中心对称.
2.用反证法证明命题“三角形中至少有一个角大于或等于60°”时,首先应假设这个三角形中( )
| A. | 有一个内角大于60° | B. | 有一个内角小于60° | ||
| C. | 每一个内角都大于60° | D. | 每一个内角都小于60° |
 将一张矩形纸条ABCD按如图所示折叠,若折叠角∠FEC=70°,则∠1=40 度;△EFG是等腰 三角形.
将一张矩形纸条ABCD按如图所示折叠,若折叠角∠FEC=70°,则∠1=40 度;△EFG是等腰 三角形.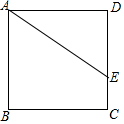 如图,正方形ABCD中,点E在DC边上,DE=4,EC=2,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则FC的长为2或10.
如图,正方形ABCD中,点E在DC边上,DE=4,EC=2,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则FC的长为2或10.