题目内容
20．计算$\sqrt{32}$÷$\sqrt{2}$×$\sqrt{3}$的结果估计在（ ）| A． | 5至6之间 | B． | 6至7之间 | C． | 7至8之间 | D． | 8至9之间 |
分析 利用二次根式的乘除法得到原式=$\sqrt{48}$，然后根据算术平方根的定义得到$\sqrt{36}$＜$\sqrt{48}$＜$\sqrt{49}$．
解答 解：原式=$\sqrt{32÷2×3}$=$\sqrt{48}$，
因为$\sqrt{36}$＜$\sqrt{48}$＜$\sqrt{49}$，
所以6＜$\sqrt{48}$＜7．
故选B．
点评 本题考查了估算无理数的大小：估算无理数大小要用逼近法．思维方法：用有理数逼近无理数，求无理数的近似值．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
8．解一元二次方程x2-8x-5=0，用配方法可变形为（ ）
| A． | （x+4）2=11 | B． | （x-4）2=11 | C． | （x+4）2=21 | D． | （x-4）2=21 |
15．
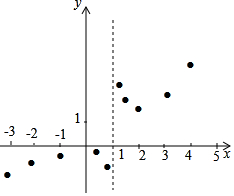有这样一个问题：探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质．
小文根据学习函数的经验，对函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质进行了探究．
下面是小文的探究过程，请补充完整：
（1）函数y=$\frac{{x}^{2}}{2x-2}$的自变量x的取值范围是x≠1；
（2）表是y与x的几组对应值．
则m的值为$\frac{9}{4}$；
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的性质（一条即可）：图象有两个分支，关于点（1，1）中心对称．
有这样一个问题：探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质．小文根据学习函数的经验，对函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质进行了探究．
下面是小文的探究过程，请补充完整：
（1）函数y=$\frac{{x}^{2}}{2x-2}$的自变量x的取值范围是x≠1；
（2）表是y与x的几组对应值．
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{7}{10}$ | $\frac{13}{10}$ | $\frac{3}{2}$ | 2 | 3 | 4 | … |
| y | … | -$\frac{9}{8}$ | -$\frac{2}{3}$ | -$\frac{1}{4}$ | 0 | -$\frac{1}{4}$ | -$\frac{49}{60}$ | $\frac{169}{60}$ | $\frac{9}{4}$ | 2 | m | $\frac{8}{3}$ | … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的性质（一条即可）：图象有两个分支，关于点（1，1）中心对称．
12．已知A，B，C三点在同一条直线上，M，N分别为线段AB，BC的中点，且AB=60，BC=40，则MN的长为（ ）
| A． | 10 | B． | 50 | C． | 10或50 | D． | 无法确定 |
9．若分式$\frac{2x}{x+3}$有意义，则x的取值范围是（ ）
| A． | x≠3 | B． | x≠-3 | C． | x＞3 | D． | x＞-3 |