题目内容
6．
如图，在Rt△ABC中，∠C=90°，AC=4，tanA=$\frac{1}{2}$，则BC的长度为（ ）| A． | 2 | B． | 8 | C． | $4\sqrt{3}$ | D． | $4\sqrt{5}$ |
分析 根据角的正切值与三角形边的关系求解．
解答 解：∵在Rt△ABC中，∠C=90°，AC=4，
∴tanA=$\frac{1}{2}$=$\frac{BC}{AC}$=$\frac{BC}{4}$，
∴BC=2．
故选A．
点评 此题考查了解直角三角形的知识，解题的关键是能够选择合适的边角关系求解，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
17．
下列四个图形中是如图展形图的立体图的是（ ）
下列四个图形中是如图展形图的立体图的是（ ）| A． |  | B． |  | C． |  | D． |  |
1．
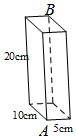如图，长方体的长为10cm，宽为5cm，高为20cm．若一只蚂蚁沿着长方体的表面从点A爬到点B，需要爬行的最短路径是（ ）
如图，长方体的长为10cm，宽为5cm，高为20cm．若一只蚂蚁沿着长方体的表面从点A爬到点B，需要爬行的最短路径是（ ）| A． | 20+5$\sqrt{5}$ | B． | 25 | C． | 10$\sqrt{5}$+5 | D． | $5\sqrt{21}$ |
18．直四棱柱、长方体和正方体之间的包含关系是（ ）
| A． |  | B． |  | C． |  | D． |  |
15．
有这样一个问题：探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质．
小文根据学习函数的经验，对函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质进行了探究．
下面是小文的探究过程，请补充完整：
（1）函数y=$\frac{{x}^{2}}{2x-2}$的自变量x的取值范围是x≠1；
（2）表是y与x的几组对应值．
则m的值为$\frac{9}{4}$；
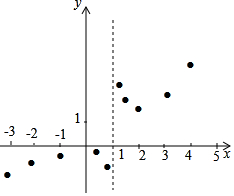
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的性质（一条即可）：图象有两个分支，关于点（1，1）中心对称．
有这样一个问题：探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质．小文根据学习函数的经验，对函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质进行了探究．
下面是小文的探究过程，请补充完整：
（1）函数y=$\frac{{x}^{2}}{2x-2}$的自变量x的取值范围是x≠1；
（2）表是y与x的几组对应值．
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{7}{10}$ | $\frac{13}{10}$ | $\frac{3}{2}$ | 2 | 3 | 4 | … |
| y | … | -$\frac{9}{8}$ | -$\frac{2}{3}$ | -$\frac{1}{4}$ | 0 | -$\frac{1}{4}$ | -$\frac{49}{60}$ | $\frac{169}{60}$ | $\frac{9}{4}$ | 2 | m | $\frac{8}{3}$ | … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的性质（一条即可）：图象有两个分支，关于点（1，1）中心对称．
16．
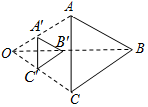如图，以点O为位似中心，将△ABC缩小后得到△A′B′C′，已知OB=3OB′，则△A′B′C′与△ABC的面积比为（ ）
如图，以点O为位似中心，将△ABC缩小后得到△A′B′C′，已知OB=3OB′，则△A′B′C′与△ABC的面积比为（ ）| A． | 1：3 | B． | 1：4 | C． | 1：8 | D． | 1：9 |