题目内容
17.是否存在整数k,使方程组$\left\{\begin{array}{l}2x+y=k\\ x-y=1\end{array}\right.$的解中,x大于1,y不大于1,则k的值为3、4、5.分析 把k看做已知数表示出方程组的解,根据x大于,y不大于1,求出k的范围,即可确定出整数k的值.
解答 解:$\left\{\begin{array}{l}{2x+y=k①}\\{x-y=1②}\end{array}\right.$,
①+②得:3x=k+1,即x=$\frac{k+1}{3}$,
①-②×2得:3y=k-2,即y=$\frac{k-2}{3}$,
根据题意得:$\left\{\begin{array}{l}{\frac{k+1}{3}>1}\\{\frac{k-2}{3}≤1}\end{array}\right.$,
解得:2<k≤5,
则整数k的值为3、4、5.
故答案为:3、4、5
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
5.已知,BD是∠ABC的角平分线.用直尺和圆规作图(不写作法,只保留作图痕迹).
(1)在线段BD上找一点P,使点P到△ABC三条边的距离相等.
(2)在线段BD上找一点Q,使点Q到点B,C的距离相等.
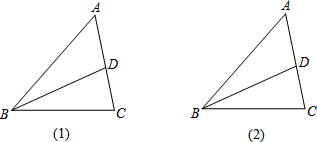
(1)在线段BD上找一点P,使点P到△ABC三条边的距离相等.
(2)在线段BD上找一点Q,使点Q到点B,C的距离相等.

12.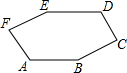 如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )
如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )
 如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )
如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )| A. | 160° | B. | 150° | C. | 145° | D. | 140° |
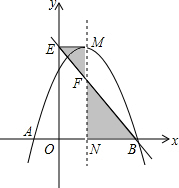 如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F.
如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F.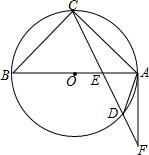 如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作⊙O的切线与CD长线交于点F,AC=8,CE:ED=6:5,AE:EB=2:3.求:
如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作⊙O的切线与CD长线交于点F,AC=8,CE:ED=6:5,AE:EB=2:3.求: