题目内容
14.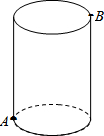 如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)
如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)
分析 首先将此圆柱展成平面图,根据两点间线段最短,可得AB最短,由勾股定理即可求得需要爬行的最短路程.
解答  解:将此圆柱展成平面图得:
解:将此圆柱展成平面图得:
∵有一圆柱,它的高等于8cm,底面直径等于4cm(π≈3),
∴AC=8cm,BC=$\frac{1}{2}$BB′=$\frac{1}{2}$×4π=6(cm),
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10(cm).
答:它需要爬行的最短路程为10cm.
点评 此题主要考查了平面展开图求最短路径问题,将圆柱体展开,根据两点之间线段最短,运用勾股定理解答是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
5.已知,BD是∠ABC的角平分线.用直尺和圆规作图(不写作法,只保留作图痕迹).
(1)在线段BD上找一点P,使点P到△ABC三条边的距离相等.
(2)在线段BD上找一点Q,使点Q到点B,C的距离相等.
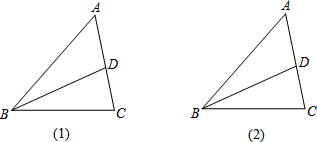
(1)在线段BD上找一点P,使点P到△ABC三条边的距离相等.
(2)在线段BD上找一点Q,使点Q到点B,C的距离相等.

19.两条平行线被第三条直线所截,则一对同位角的平分线的位置关系是( )
| A. | 互相垂直 | B. | 平行 | ||
| C. | 相交但不垂直 | D. | 平行或相交都有可能 |
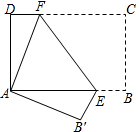 如图,将矩形纸片ABCD折叠,使点C与点A重合(折痕为EF),剪去不折叠的部分.
如图,将矩形纸片ABCD折叠,使点C与点A重合(折痕为EF),剪去不折叠的部分.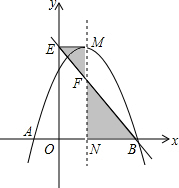 如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F.
如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F.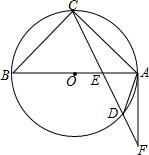 如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作⊙O的切线与CD长线交于点F,AC=8,CE:ED=6:5,AE:EB=2:3.求:
如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作⊙O的切线与CD长线交于点F,AC=8,CE:ED=6:5,AE:EB=2:3.求: