题目内容
15.观察下列三个特殊的等式:1×2=$\frac{1}{3}$(1×2×3-0×1×2),2×3=$\frac{1}{3}$(2×3×4-1×2×3),3×4=$\frac{1}{3}$(3×4×5-2×3×4)将这三个等式的两边相加,可以得到1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20.请你思考后回答:
(1)1×2+2×3+…+100×101=343400;
(2)1×2+2×3+…+n(n+1)=$\frac{1}{3}$n(n+1)(n+2).
分析 (1)根据1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20可以得出,连续两个自然数的乘积的和等于后面一个算式的两个数字再与最后一个数字加1相乘积的$\frac{1}{3}$,据此可计算1×2+2×3+…+100×101;
(2)由此得出一般性规律1×2+2×3+…+n(n+1)=$\frac{1}{3}$n(n+1)(n+2)即可解决问题.
解答 解:(1)∵1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=$\frac{1}{3}$×4×5=20,
∴1×2+2×3+…+100×101=$\frac{1}{3}$×100×101×102=343400;
(2)1×2+2×3+3×4+…+n×(n+1)=$\frac{1}{3}$n(n+1)( n+2).
故答案为:(1)343400;(2)$\frac{1}{3}$n(n+1)(n+2).
点评 此题主要考查了数字的规律性问题,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,很容易发现各部分的变化规律,但是如何用一个统一的式子表示出变化规律是难点中的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知,BD是∠ABC的角平分线.用直尺和圆规作图(不写作法,只保留作图痕迹).
(1)在线段BD上找一点P,使点P到△ABC三条边的距离相等.
(2)在线段BD上找一点Q,使点Q到点B,C的距离相等.
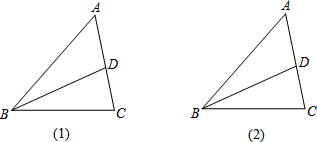
(1)在线段BD上找一点P,使点P到△ABC三条边的距离相等.
(2)在线段BD上找一点Q,使点Q到点B,C的距离相等.

10.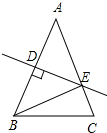 在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )
在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )
 在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )
在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 如图,平移△ABC可得到△DEF,若∠A=45°,∠C=65°,则∠E=70°,∠EDF=45°,∠DOB=65°.
如图,平移△ABC可得到△DEF,若∠A=45°,∠C=65°,则∠E=70°,∠EDF=45°,∠DOB=65°.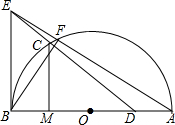 如图,在半径为2的⊙O中,AB是直径,C是弧AB的三等分点(∠BOC为锐角),D是OA的中点,BE是⊙O的切线,B为切点,DC的延长线交BE于点E,连接AE,交⊙O于点F.
如图,在半径为2的⊙O中,AB是直径,C是弧AB的三等分点(∠BOC为锐角),D是OA的中点,BE是⊙O的切线,B为切点,DC的延长线交BE于点E,连接AE,交⊙O于点F.