题目内容
7.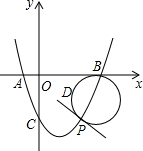 如图,抛物线y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D的坐标为(1,-1),P是第四象限内抛物线上一动点,以PB为直径的圆经过点D,求经过点P且和这个圆相切的直线的解析式.
如图,抛物线y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D的坐标为(1,-1),P是第四象限内抛物线上一动点,以PB为直径的圆经过点D,求经过点P且和这个圆相切的直线的解析式.
分析 根据题意可以求得线段PB的中点坐标,然后根据以PB为直径的圆经过点D,P是第四象限内抛物线上一动点,可以求得点P的坐标,从而可以求得经过点P且和这个圆相切的直线的解析式.
解答 解:∵y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D的坐标为(1,-1),P是第四象限内抛物线上一动点,
∴设点P的坐标为(a,a2-2a-3),
∴线段PB的中点坐标是($\frac{a+3}{2},\frac{{a}^{2}-2a-3}{2}$),
∵以PB为直径的圆经过点D,
∴$\sqrt{(\frac{{a}^{2}-2a-3}{2}+1)^{2}+(\frac{a+3}{2}-1)^{2}}$=$\frac{\sqrt{({a}^{2}-2a-3-0)^{2}+(a-3)^{2}}}{2}$,
解得,a=2或a=-2(舍去),
∴点P的坐标是(2,-3),
设过点P(2,-3)和点B(3,0)的直线的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{2k+b=-3}\\{3k+b=0}\end{array}\right.$
解得,$\left\{\begin{array}{l}{k=3}\\{b=-9}\end{array}\right.$
即过点P(2,-3)和点B(3,0)的直线的解析式为y=3x-9,
∴可设过点P(2,-3)且和这个圆相切的直线的解析式为:y=-$\frac{1}{3}x+c$,
∴-3=$-\frac{1}{3}×2+c$,得c=$-\frac{7}{3}$,
即过点P且和这个圆相切的直线的解析式为:y=$-\frac{1}{3}x-\frac{7}{3}$.
点评 本题考查抛物线与x轴的交点坐标,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

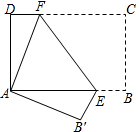 如图,将矩形纸片ABCD折叠,使点C与点A重合(折痕为EF),剪去不折叠的部分.
如图,将矩形纸片ABCD折叠,使点C与点A重合(折痕为EF),剪去不折叠的部分.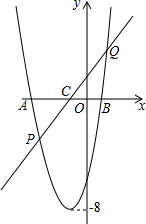 如图,已知二次函数的最小值是-8,它的图象与x轴交于A(-3,0)、B(1,0)两点,一次函数y=kx+b(k>0)的图象过点C(-1,0),且与该二次函数的图象交于P、Q两点.
如图,已知二次函数的最小值是-8,它的图象与x轴交于A(-3,0)、B(1,0)两点,一次函数y=kx+b(k>0)的图象过点C(-1,0),且与该二次函数的图象交于P、Q两点.