题目内容
10.如图,顶点为M的抛物线y=a(x+1)2-4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,-3).(1)求抛物线的函数表达式;
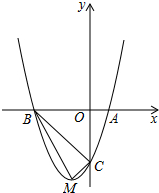
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
分析 (1)用待定系数法求出抛物线解析式即可;
(2)由抛物线解析式确定出抛物线的顶点坐标和与x轴的交点坐标,用勾股定理的逆定理即可;
(3)根据题意判断出点N只能在x轴上方的抛物线上,由已知四边形的面积相等转化出S△ABN=S△BCM,然后求出三角形BCM的面积,再建立关于点N的坐标的方程求解即可.
解答 解:(1)∵抛物线y=a(x+1)2-4与y轴相交于点C(0,-3).
∴-3=a-4,
∴a=1,
∴抛物线解析式为y=(x+1)2-4=x2+2x-3,
(2)△BCM是直角三角形
理由:由(1)有,抛物线解析式为y=(x+1)2-4,
∵顶点为M的抛物线y=a(x+1)2-4,
∴M(-1,-4),
由(1)抛物线解析式为y=x2+2x-3,
令y=0,
∴x2+2x-3=0,
∴x1=-3,x2=1,
∴A(1,0),B(-3,0),
∴BC2=9+9=18,CM2=1+1=2,BM2=4+16=20,
∴BC2+CM2=BM2,
∴△BCM是直角三角形,
(3)存在,N(-1+$\frac{\sqrt{22}}{2}$,$\frac{3}{2}$)或N(-1-$\frac{\sqrt{22}}{2}$,$\frac{3}{2}$),
∵以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等,且点M是抛物线的顶点,
∴①点N在x轴上方的抛物线上,
如图,
由(2)有△BCM是直角三角形,BC2=18,CM2=2,
∴BC=3$\sqrt{2}$,CM=$\sqrt{2}$,
∴S△BCM=$\frac{1}{2}$BC×CM=$\frac{1}{2}$×3$\sqrt{2}$×$\sqrt{2}$=3,
设N(m,n),
∵以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等,
∴S△ABN+S△ABC=S△BCM+S△ABC,
∴S△ABN=S△BCM=3,
∵A(1,0),B(-3,0),
∴AB=4,
∴S△ABN=$\frac{1}{2}$×AB×n=$\frac{1}{2}$×4×n=2n=3,
∴n=$\frac{3}{2}$,
∵N在抛物线解析式为y=x2+2x-3的图象上,
∴m2+2m-3=$\frac{3}{2}$,
∴m1=-1+$\frac{\sqrt{22}}{2}$,m2=-1-$\frac{\sqrt{22}}{2}$,
∴N(-1+$\frac{\sqrt{22}}{2}$,$\frac{3}{2}$)或N(-1-$\frac{\sqrt{22}}{2}$,$\frac{3}{2}$).
②如图2,
②点N在x轴下方的抛物线上,
∵点C在对称轴的右侧,
∴点N在对称轴右侧不存在,只有在对称轴的左侧,
过点M作MN∥BC,交抛物线于点N,
∵B(-3,0),C(0,-3),
∴直线BC解析式为y=-x-3,
设MN的解析式为y=-x+b
∵抛物线解析式为y=(x+1)2-4①,
∴M(-1,-4),
∴直线MN解析式为y=-x-5②,
联立①②得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=-4}\end{array}\right.$(舍),$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-3}\end{array}\right.$,
∴N(-2,-3),
即:N(-1+$\frac{\sqrt{22}}{2}$,$\frac{3}{2}$)或N(-1-$\frac{\sqrt{22}}{2}$,$\frac{3}{2}$)或N(-2,-3).
点评 此题是二次函数综合题,主要考查了待定系数法求抛物线解析式,直角三角形的判断,图形面积的计算,解本题的关键是判断出△BCM是直角三角形,难点是要两个四边形面积相等,点N分在x轴上方的抛物线上和下方的抛物线上,用方程的思想解决问题是解决(3)的关键,也是初中阶段常用的方法.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | m≤2 | B. | m≥2 | C. | m≤1 | D. | m>1 |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | 七边形 | B. | 八边形 | C. | 九边形 | D. | 十边形 |
 一次函数y=kx+3的图象如图所示,当y<0时,x的取值范围是( )
一次函数y=kx+3的图象如图所示,当y<0时,x的取值范围是( )| A. | x<0 | B. | x>0 | C. | x<2 | D. | x>2 |
| A. | 3cm | B. | 8cm | C. | 10cm | D. | 无法确定 |
| A. |  | B. |  | C. |  | D. |  |
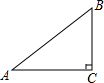 如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )
如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )| A. | $\frac{BC}{AB}$ | B. | $\frac{BC}{AC}$ | C. | $\frac{AC}{AB}$ | D. | $\frac{AC}{BC}$ |