题目内容
4. 如图,已知AB∥CD∥EF,则x、y、z三者之间的关系是( )
如图,已知AB∥CD∥EF,则x、y、z三者之间的关系是( )| A. | x+y+z=180° | B. | x+y-z=180° | C. | y-x-z=0° | D. | y-x-2z=0° |
分析 根据平行线的性质可得∠CEF=180°-y,x=z+∠CEF,利用等量代换可得x=z+180°-y,再变形即可.
解答 解:∵CD∥EF,
∴∠C+∠CEF=180°,
∴∠CEF=180°-y,
∵AB∥CD,
∴x=z+∠CEF,
∴x=z+180°-y,
∴x+y-z=180°,
故选:B.
点评 此题主要考查了平行线的性质,关键是掌握平行线性质定理:
定理1:两条平行线被第三条直线所截,同位角相等. 简单说成:两直线平行,同位角相等.
定理2:两条平行线被地三条直线所截,同旁内角互补..简单说成:两直线平行,同旁内角互补.
定理3:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.

练习册系列答案
相关题目
15.将长度为3cm的线段向上平移10cm,再向右平移8cm,所得线段的长是( )
| A. | 3cm | B. | 8cm | C. | 10cm | D. | 无法确定 |
9.若点P(2014,a)、Q(2015,b)都在函数y=$\frac{2016}{x}$的图象上,则下列结论中正确的是( )
| A. | a>b | B. | a=b | ||
| C. | a<b | D. | a、b的大小关系无法确定 |
16.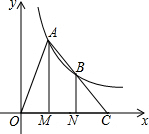 如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
 如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
13. 如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )
如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )
 如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )
如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )| A. | 40° | B. | 50° | C. | 140° | D. | 130° |
14. 如图,直线l1∥l2,等腰直角△ABC的两个顶点A、B分别落在直线l1、l2上,∠ACB=90°,若∠1=15°,则∠2的度数是( )
如图,直线l1∥l2,等腰直角△ABC的两个顶点A、B分别落在直线l1、l2上,∠ACB=90°,若∠1=15°,则∠2的度数是( )
 如图,直线l1∥l2,等腰直角△ABC的两个顶点A、B分别落在直线l1、l2上,∠ACB=90°,若∠1=15°,则∠2的度数是( )
如图,直线l1∥l2,等腰直角△ABC的两个顶点A、B分别落在直线l1、l2上,∠ACB=90°,若∠1=15°,则∠2的度数是( )| A. | 35° | B. | 30° | C. | 25° | D. | 20° |