题目内容
11.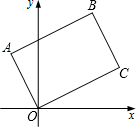 将矩形OABC如图放置,O为原点.若点A(-1,2),点B的纵坐标是$\frac{7}{2}$,则点C的坐标是( )
将矩形OABC如图放置,O为原点.若点A(-1,2),点B的纵坐标是$\frac{7}{2}$,则点C的坐标是( )| A. | (4,2) | B. | (2,4) | C. | ($\frac{3}{2}$,3) | D. | (3,$\frac{3}{2}$) |
分析 首先构造直角三角形,利用相似三角形的判定与性质以及结合全等三角形的判定与性质得出CM=$\frac{3}{2}$,MO=3,进而得出答案.
解答  解:过点A作AE⊥x轴于点E,过点B作BF⊥⊥x轴于点F,过点A作AN⊥BF于点N,
解:过点A作AE⊥x轴于点E,过点B作BF⊥⊥x轴于点F,过点A作AN⊥BF于点N,
过点C作CM⊥x轴于点M,
∵∠EAO+∠AOE=90°,∠AOE+∠MOC=90°,
∴∠EAO=∠COM,
又∵∠AEO=∠CMO,
∴∠AEO∽△COM,
∴$\frac{EO}{AE}$=$\frac{CM}{MO}$,
∵∠BAN+∠OAN=90°,∠EAO+∠OAN=90°,
∴∠BAN=∠EAO=∠COM,
在△ABN和△OCM中
$\left\{\begin{array}{l}{∠BNA=∠CMO}\\{∠BAN=∠COM}\\{AB=OC}\end{array}\right.$,
∴△ABN≌△OCM(AAS),
∴BN=CM,
∵点A(-1,2),点B的纵坐标是$\frac{7}{2}$,
∴BN=$\frac{3}{2}$,
∴CM=$\frac{3}{2}$,
∴MO=3,
∴点C的坐标是:(3,$\frac{3}{2}$).
故选:D.
点评 此题主要考查了矩形的性质以及相似三角形的判定与性质以及结合全等三角形的判定与性质等知识,正确得出CM的长是解题关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
1.下面给出了6个式子:①3>0;②4x+3y>0;③x=3;④x-1;⑤x+2≤3;⑥2x≠0,其中不等式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.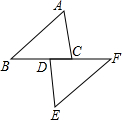 如图,已知AB∥EF,AB=EF,则下列条件中,不能作为判断△ABC≌△EFD的是( )
如图,已知AB∥EF,AB=EF,则下列条件中,不能作为判断△ABC≌△EFD的是( )
 如图,已知AB∥EF,AB=EF,则下列条件中,不能作为判断△ABC≌△EFD的是( )
如图,已知AB∥EF,AB=EF,则下列条件中,不能作为判断△ABC≌△EFD的是( )| A. | AC∥DE | B. | AC=DE | C. | BD=CF | D. | ∠A=∠E |
16.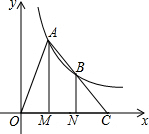 如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
 如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
20.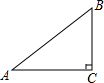 如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )
如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )
 如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )
如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )| A. | $\frac{BC}{AB}$ | B. | $\frac{BC}{AC}$ | C. | $\frac{AC}{AB}$ | D. | $\frac{AC}{BC}$ |