题目内容
8. 如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )
如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )| A. | 30° | B. | 40° | C. | 70° | D. | 80° |
分析 根据三角形内角和定理求出∠BAC,根据全等三角形的对应角相等得出∠DAE=∠BAC=70°,∠E=∠C=30°,又由∠DAB:∠DAC=4:3,求出∠DAC=30°,那么∠EAC=∠DAE-∠DAC=40°,再根据三角形外角的性质得出∠EFC的度数.
解答 解:∵∠B=80°,∠C=30°,
∴∠BAC=180°-∠B-∠C=70°,
∵△ABC≌△ADE,
∴∠DAE=∠BAC=70°,∠E=∠C=30°.
∵∠DAB:∠DAC=4:3,
∴∠DAB=40°,∠DAC=30°,
∴∠EAC=∠DAE-∠DAC=70°-30°=40°,
∴∠EFC=∠E+∠EAC=30°+40°=70°.
故选C.
点评 本题考查了全等三角形的性质,三角形内角和定理,三角形外角的性质,注意:全等三角形的对应角相等,对应边相等.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
18.正n边形的每一个外角都不大于40°,则满足条件的多边形边数最少为( )
| A. | 七边形 | B. | 八边形 | C. | 九边形 | D. | 十边形 |
16.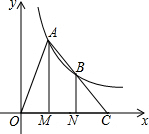 如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
 如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
13. 如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )
如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )
 如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )
如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )| A. | 40° | B. | 50° | C. | 140° | D. | 130° |
20.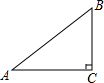 如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )
如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )
 如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )
如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )| A. | $\frac{BC}{AB}$ | B. | $\frac{BC}{AC}$ | C. | $\frac{AC}{AB}$ | D. | $\frac{AC}{BC}$ |
17.把抛物线y=-$\frac{1}{2}{x^2}$经( )平移得到y=-$\frac{1}{2}{(x-2)^2}$-1.
| A. | 向右平移2个单位,向上平移1个单位 | |
| B. | 向右平移2个单位,向下平移1个单位 | |
| C. | 向左平移2个单位,向上平移1个单位 | |
| D. | 向左平移2个单位,向下平移1个单位 |
18.下列运算正确的是( )
| A. | (a2)5=a7 | B. | a2•a3=a5 | C. | (ab)2=a2b | D. | 3ab-2b=a |