题目内容
11.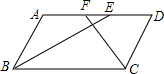 如图,在?ABCD中,BE平分∠ABC交AD于点E,CF平分∠BCD交AD于点F,AB=3,AD=5,则EF的长为1.
如图,在?ABCD中,BE平分∠ABC交AD于点E,CF平分∠BCD交AD于点F,AB=3,AD=5,则EF的长为1.
分析 根据平行四边形的性质可知∠AEB=∠EBC,又因为BE平分∠ABC,所以∠ABE=∠EBC,则∠ABE=∠AEB,则AB=AE=3,同理可证FD=3,继而可求得EF=AE+DE-AD.
解答 解:∵四边形ABCD是平行四边形,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
则∠ABE=∠AEB,
∴AB=AE=3,
同理可证:DF=DC=AB=3,
则EF=AE+FD-AD=3+3-5=1.
故答案为:1.
点评 本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
20.下列由左到右的变形中属于因式分解的是( )
| A. | 24x2y=3x•8xy | B. | m2-2m-3=m(m-2)-3 | C. | x2+2x+1=(x+1)2 | D. | (x+3)(x-3)=x2-9 |
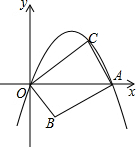 如图,在平面直角坐标系中,抛物线y=-x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,-1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC.
如图,在平面直角坐标系中,抛物线y=-x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,-1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC. 如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长为2.
如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长为2.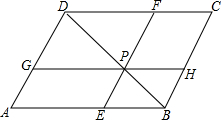 如图,在?ABCD中,P是对角线BD上的一点,过P点的直线EF∥BC.GH∥AB.则图中面积相等的四边形有5对.
如图,在?ABCD中,P是对角线BD上的一点,过P点的直线EF∥BC.GH∥AB.则图中面积相等的四边形有5对. 已知:如图,Rt△ABC中,∠BAC=90°,AB=5,AC=12,将△ABC沿射线BC方向平移m个单位长度到△DEF,顶点A、B、C分别与D、E、F对应,若以点A、D、E为顶点的三角形是等腰三角形,则m的值是$\frac{50}{13}$、5或$\frac{13}{2}$.
已知:如图,Rt△ABC中,∠BAC=90°,AB=5,AC=12,将△ABC沿射线BC方向平移m个单位长度到△DEF,顶点A、B、C分别与D、E、F对应,若以点A、D、E为顶点的三角形是等腰三角形,则m的值是$\frac{50}{13}$、5或$\frac{13}{2}$.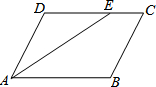 如图:在?ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=27°,求∠C、∠B的度数.
如图:在?ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=27°,求∠C、∠B的度数.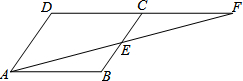 如图,?ABCD中,E是BC的中点,连结AE并延长交DC的延长线于F.试问:AB与CF相等吗?请说明理由.
如图,?ABCD中,E是BC的中点,连结AE并延长交DC的延长线于F.试问:AB与CF相等吗?请说明理由.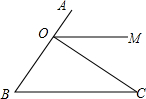 如图,已知∠B=50°,∠BOC=80°,OM平分∠AOC,求证:OM∥BC.
如图,已知∠B=50°,∠BOC=80°,OM平分∠AOC,求证:OM∥BC.