题目内容
已知一次函数y=kx+b(k≠0)和反比例函数y=
的图象交于点A(1,1).
(1)求两个函数的表达式.
(2)若点B(3,0),则△AOB得到面积是多少?直接写出结论.
| k |
| 2x |
(1)求两个函数的表达式.
(2)若点B(3,0),则△AOB得到面积是多少?直接写出结论.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把A的坐标代入y=
,求出k的值得到反比例函数解析式;再把k的值及A的坐标代入y=kx+b,求出b的值,得到一次函数的解析式即可;
(2)根据三角形的面积公式即可求出△AOB的面积.
| k |
| 2x |
(2)根据三角形的面积公式即可求出△AOB的面积.
解答:解:(1)∵点A(1,1)在反比例函数y=
的图象上,
∴k=2×1×1=2,
∴反比例函数的表达式为y=
;
把点A(1,1),k=2代入一次函数y=kx+b中,
得1=2+b,
解得:b=-1,
∴一次函数的表达式为y=2x-1,
故反比例函数的表达式是y=
,一次函数的表达式是y=2x-1;
(2)∵A(1,1),B(3,0),
∴S△AOB=
×3×1=1.5.
故△AOB的面积是1.5.
| k |
| 2x |
∴k=2×1×1=2,
∴反比例函数的表达式为y=
| 1 |
| x |
把点A(1,1),k=2代入一次函数y=kx+b中,
得1=2+b,
解得:b=-1,
∴一次函数的表达式为y=2x-1,
故反比例函数的表达式是y=
| 1 |
| x |
(2)∵A(1,1),B(3,0),
∴S△AOB=
| 1 |
| 2 |
故△AOB的面积是1.5.
点评:本题主要考查对用待定系数法求一次函数、反比例函数的解析式,解一元一次方程,一次函数图象上点的坐标特征,三角形的面积等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.

练习册系列答案
相关题目
 如图,用∠B=∠D,∠1=∠2直接判定△ABC≌△ADC的理由是( )
如图,用∠B=∠D,∠1=∠2直接判定△ABC≌△ADC的理由是( )| A、AAS | B、SSS |
| C、ASA | D、SAS |
 如图所示,在Rt△ABC中,∠ACB=90°,AB=BC=2,将Rt△ABC绕A点逆时针旋转45°后得到Rt△ADE,则CD=
如图所示,在Rt△ABC中,∠ACB=90°,AB=BC=2,将Rt△ABC绕A点逆时针旋转45°后得到Rt△ADE,则CD=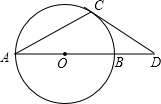 如图:已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10.
如图:已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10.