题目内容
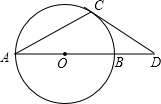 如图:已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10.
如图:已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10.(1)求证:AC=CD;
(2)求⊙O的面积.
考点:切线的性质
专题:计算题
分析:(1)连结OC,如图,根据切线的性质得OC⊥CD,则∠OCD=90°,所以∠ACO=∠ACD-∠OCD=30°,则∠A=∠ACO=30°,接着利用三角形内角和定理计算出∠D=30°,然后根据等腰三角形的判定定理即可得到AC=CD;
(2)在Rt△OCD中利用含30度的直角三角形三边的关系得到OD=2OC,则OB+10=2OB,解得OB=10,然后根据圆的面积公式求解.
(2)在Rt△OCD中利用含30度的直角三角形三边的关系得到OD=2OC,则OB+10=2OB,解得OB=10,然后根据圆的面积公式求解.
解答:(1)证明:连结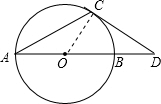 OC,如图,
OC,如图,
∵CD切⊙O于点C,
∴OC⊥CD,
∴∠OCD=90°,
∵∠ACD=120°,
∴∠ACO=∠ACD-∠OCD=30°,
而OC=OA,
∴∠A=∠ACO=30°,
∵∠D=180°-∠ACD-∠A=30°,
∴∠A=∠D,
∴AC=CD;
(2)解:在Rt△OCD中,∵∠D=30°,
∴OD=2OC,
而OC=OB,
∴OB+10=2OB,解得OB=10,
∴⊙O的面积=π•102=100π.
 OC,如图,
OC,如图,∵CD切⊙O于点C,
∴OC⊥CD,
∴∠OCD=90°,
∵∠ACD=120°,
∴∠ACO=∠ACD-∠OCD=30°,
而OC=OA,
∴∠A=∠ACO=30°,
∵∠D=180°-∠ACD-∠A=30°,
∴∠A=∠D,
∴AC=CD;
(2)解:在Rt△OCD中,∵∠D=30°,
∴OD=2OC,
而OC=OB,
∴OB+10=2OB,解得OB=10,
∴⊙O的面积=π•102=100π.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
抛物线y=-x2+2x-1的顶点坐标是( )
| A、(1,0) |
| B、(-1,0) |
| C、(-2,0) |
| D、(2,-1) |
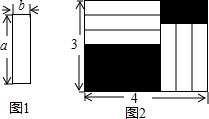 如图1是长为a,宽为b的小长方形卡片,把六张这样的小长方形卡片不重叠地放在一个底面为长方形(长为4,宽为3)的盒子底部(如图2),盒子底部未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长之和为( )
如图1是长为a,宽为b的小长方形卡片,把六张这样的小长方形卡片不重叠地放在一个底面为长方形(长为4,宽为3)的盒子底部(如图2),盒子底部未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长之和为( )| A、8 | B、10 | C、12 | D、14 |
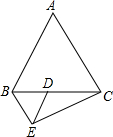 已知:如图,△ABC和△BDE均为等边三角形,B、D、C三点在一条直线上,AC⊥CE,判断线段DE与AC的数量关系,并加以证明.
已知:如图,△ABC和△BDE均为等边三角形,B、D、C三点在一条直线上,AC⊥CE,判断线段DE与AC的数量关系,并加以证明.