题目内容
7.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过1000元后,超出1000元的部分按90%收费;在乙商场累计购物超过500元后,超出500元的部分按95%收费,设小红在同一商场累计购物x元,其中x>1000.(1)根据题题意,填写下表(单位:元)
| 累计购物 | 1300 | 2900 | … | x |
| 在甲商场实际花费 | 1270 | 2710 | … | 0.9x+100 |
| 在乙商场实际花费 | 1260 | 2780 | … | 0.95x+25 |
(3)当小红在同一商场累计购物超过1000元时,在哪家商场的实际花费少?
分析 (1)根据已知得出甲商场1000+(2900-1000)×0.9以及500+(2900-500)×0.95进而得出答案,同理可得出在乙商场累计购物2900元、x元的实际花费;
(2)根据题中已知条件,求出0.95x+2.5,0.9x+100相等,从而得出正确结论;
(3)根据0.95x+25与0.9x+100相比较,从而得出正确结论.
解答 解:(1)在甲商场:1000+(1300-1000)×0.9=1270,
1000+(2900-1000)×0.9=2710,
1000+(x-1000)×0.9=0.9x+100;
在乙商场:500+(1300-500)×0.95=1260,
500+(2900-500)×0.95=2780,
500+(x-500)×0.95=0.95x+25;
填表如下:
| 累计购物 | 1300 | 2900 | … | x |
| 在甲商场实际花费 | 1270 | 2710 | … | 0.9x+100 |
| 在乙商场实际花费 | 1260 | 2780 | … | 0.95x+25 |
0.9x+100=0.95x+25,
解得:x=1500,
答:当x为1500时,小红在甲、乙两商场的实际花费相同;
(3)由0.9x+100<0.95x+25,
解得:x>1500,
0.9x+100>0.95x+25,
解得:x<1500,
∴当小红累计购物大于1500时,选择甲商场实际花费少;
当累计购物正好为1500元时,两商场花费相同;
当小红累计购物超过1000元而不到1500元时,在乙商场实际花费少.
答:当小红累计购物超过1000元而不到1500元时,在乙商场实际花费少;正好为1500元时,两商场花费相同;大于1500时,选择甲商场实际花费少.
点评 此题主要考查了一元一次不等式的应用和一元一次方程的应用,此题问题较多且不是很简单,有一定难度.涉及方案选择时应与方程或不等式联系起来.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
2.解关于x的不等式组$\left\{\begin{array}{l}{x-a<0}\\{7-2x≤2}\end{array}\right.$的整数解有4个,则a的取值范围是( )
| A. | 6<a<7 | B. | 6≤a<7 | C. | 6≤a≤7 | D. | 6<a≤7 |
 如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为A(6,3),B(0,5).
如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为A(6,3),B(0,5).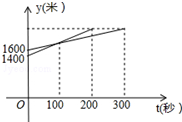 一次越野赛跑中,当甲跑了1600米时,乙跑了1400米,甲、乙在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示:
一次越野赛跑中,当甲跑了1600米时,乙跑了1400米,甲、乙在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示: