题目内容
2.解关于x的不等式组$\left\{\begin{array}{l}{x-a<0}\\{7-2x≤2}\end{array}\right.$的整数解有4个,则a的取值范围是( )| A. | 6<a<7 | B. | 6≤a<7 | C. | 6≤a≤7 | D. | 6<a≤7 |
分析 先根据一元一次不等式组解出x的取值,再根据不等式组$\left\{\begin{array}{l}{x-a<0}\\{7-2x≤2}\end{array}\right.$的整数解有4个,求出实数a的取值范围.
解答 解:$\left\{\begin{array}{l}{x-a<0①}\\{7-2x≤2②}\end{array}\right.$,
由①得:x<a,
由②得:x≥$\frac{5}{2}$,
∴不等式组的解集为:$\frac{5}{2}$≤x<a,
∵只有4个整数解,
∴整数解为:3,4,5,6,
∴6<a≤7.
故选D.
点评 本题考查了一元一次不等式组的整数解.关键是先解每一个不等式,再根据整数解的个数,确定含a的代数式的取值范围.

练习册系列答案
相关题目
10.下列选项中,∠MOP与∠NOP是邻补角的是( )
| A. |  | B. |  | C. |  | D. |  |
7.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过1000元后,超出1000元的部分按90%收费;在乙商场累计购物超过500元后,超出500元的部分按95%收费,设小红在同一商场累计购物x元,其中x>1000.
(1)根据题题意,填写下表(单位:元)
(2)当x取何值时,小红在甲、乙两商场的实际花费相同?
(3)当小红在同一商场累计购物超过1000元时,在哪家商场的实际花费少?
(1)根据题题意,填写下表(单位:元)
| 累计购物 | 1300 | 2900 | … | x |
| 在甲商场实际花费 | 1270 | 2710 | … | 0.9x+100 |
| 在乙商场实际花费 | 1260 | 2780 | … | 0.95x+25 |
(3)当小红在同一商场累计购物超过1000元时,在哪家商场的实际花费少?
14.在平面直角坐标系xOy中,点P(-3,5)关于x轴的对称点的坐标是( )
| A. | (3,5) | B. | (3,-5) | C. | (5,-3) | D. | (-3,-5) |
9.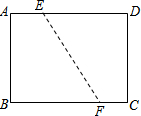 如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使B点与D点重合,则折痕EF的长是( )
如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使B点与D点重合,则折痕EF的长是( )
 如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使B点与D点重合,则折痕EF的长是( )
如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使B点与D点重合,则折痕EF的长是( )| A. | 6 | B. | $\frac{15}{4}$ | C. | 5 | D. | $\frac{15}{2}$ |
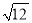 ︱+(
︱+(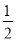 )-2;
)-2;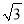 x-
x-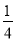 = 0.
= 0.