题目内容
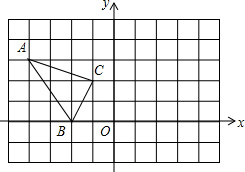
17. 如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为A(6,3),B(0,5).
如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为A(6,3),B(0,5).(1)画出△OAB绕原点O逆时针方向旋转90°后得到的△OA1B1;
(2)画出△OAB关于原点O的中心对称图形△OA2B2;
(3)猜想:∠OAB的度数为多少?并说明理由.
分析 (1)根据旋转的性质得出对应点位置,进而得出答案;
(2)根据中心对称的性质得出对应点位置,进而得出答案;
(3)∠OAB=45°,根据A1(-3,6),A(6,3),可根据勾股定理求出OA=OA1=3$\sqrt{5}$,又∠AOA1=90°,易证△A1AO为等腰直角三角形,得∠OAB=45°.
解答 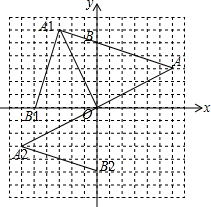 解:(1)如图所示,△OA1B1即为所求;
解:(1)如图所示,△OA1B1即为所求;
(2)如图所示△OA2B2即为所求;
(3)∠OAB=45°,
理由:∵A1(-3,6),A(6,3)
∴OA=OA1=3$\sqrt{5}$,
又∵∠AOA1=90°,
∴△A1AO为等腰直角三角形,
∴∠OAB=45°.
点评 此题主要考查了图形的旋转、中心对称以及勾股定理,得出旋转后对应点位置是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过1000元后,超出1000元的部分按90%收费;在乙商场累计购物超过500元后,超出500元的部分按95%收费,设小红在同一商场累计购物x元,其中x>1000.
(1)根据题题意,填写下表(单位:元)
(2)当x取何值时,小红在甲、乙两商场的实际花费相同?
(3)当小红在同一商场累计购物超过1000元时,在哪家商场的实际花费少?
(1)根据题题意,填写下表(单位:元)
| 累计购物 | 1300 | 2900 | … | x |
| 在甲商场实际花费 | 1270 | 2710 | … | 0.9x+100 |
| 在乙商场实际花费 | 1260 | 2780 | … | 0.95x+25 |
(3)当小红在同一商场累计购物超过1000元时,在哪家商场的实际花费少?
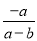 可变形为( )
可变形为( )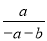 B.
B. 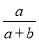 C.
C. 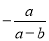 D.
D. 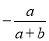
 在平面直角坐标内点A(-4、3),B(-2、0),C(-1,2),将△ABC绕点O顺时针旋转90°后得到△A′B′C′.
在平面直角坐标内点A(-4、3),B(-2、0),C(-1,2),将△ABC绕点O顺时针旋转90°后得到△A′B′C′.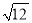 ︱+(
︱+(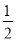 )-2;
)-2;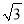 x-
x-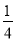 = 0.
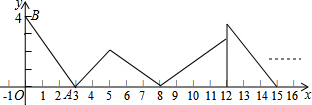
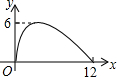
= 0.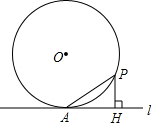 如图,过半径为6的圆O上一点A作圆O的切线l,P为圆O的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x的函数关系的是( )
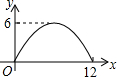
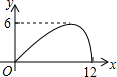
如图,过半径为6的圆O上一点A作圆O的切线l,P为圆O的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x的函数关系的是( )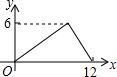
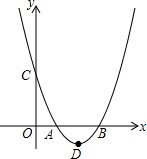 在平面直角坐标系中,抛物线y1=ax2-4ax+n与x轴的交点A、B,抛物线的顶点为D.
在平面直角坐标系中,抛物线y1=ax2-4ax+n与x轴的交点A、B,抛物线的顶点为D.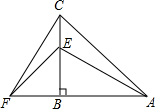 在△ACF中,CB⊥FA于点B,BE=BF,BA=BC.
在△ACF中,CB⊥FA于点B,BE=BF,BA=BC.