题目内容
7.已知一次函数的图象经过A(0,3),B(2,9)两点.(1)求这个一次函数的表达式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上.
分析 (1)根据点A、B的坐标,利用待定系数法即可求出直线AB的表达式;
(2)将x=-1代入一次函数表达式中求出y值,由该y值不等于1,即可得出点P不在这个一次函数的图象上.
解答 解:(1)设直线AB的表达式为y=kx+b(k≠0),
将点A(0,3)、B(2,9)代入y=kx+b,
得:$\left\{\begin{array}{l}{b=3}\\{2k+b=9}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=3}\\{b=3}\end{array}\right.$,
∴直线AB的表达式为y=3x+3.
(2)∵当x=-1时,y=3x+3=0≠1,
∴点P不在这个一次函数的图象上.
点评 本题考查了待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,解题的关键是:(1)根据点的坐标,利用待定系数法求出一次函数表达式;(2)利用一次函数图象上点的坐标特征验证点P是否在该一次函数图象上.

练习册系列答案
相关题目
17.计算5-2正确的是( )
| A. | -10 | B. | $-\frac{1}{25}$ | C. | $\frac{1}{25}$ | D. | 25 |
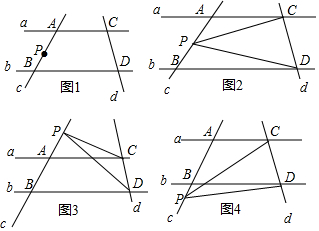
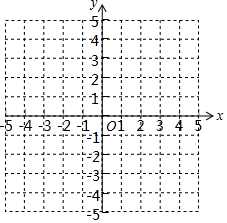 已知A(-3,-2),B(2,-2),C(3,1),D(-2,1)四个点.
已知A(-3,-2),B(2,-2),C(3,1),D(-2,1)四个点.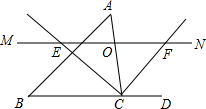 如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠ACB的外角平分线CF于点F,交∠ACB内角平分线CE于E.
如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠ACB的外角平分线CF于点F,交∠ACB内角平分线CE于E. 如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b≤kx+4的解集是x≤1.
如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b≤kx+4的解集是x≤1.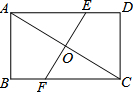 如图,在矩形ABCD中,AD=4,CD=3,对角线AC的垂直平分线分别交AD、BC于点E、F,垂足为O,则EF的长为$\frac{15}{4}$.
如图,在矩形ABCD中,AD=4,CD=3,对角线AC的垂直平分线分别交AD、BC于点E、F,垂足为O,则EF的长为$\frac{15}{4}$.