题目内容
17.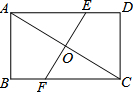 如图,在矩形ABCD中,AD=4,CD=3,对角线AC的垂直平分线分别交AD、BC于点E、F,垂足为O,则EF的长为$\frac{15}{4}$.
如图,在矩形ABCD中,AD=4,CD=3,对角线AC的垂直平分线分别交AD、BC于点E、F,垂足为O,则EF的长为$\frac{15}{4}$.
分析 设AE=x,则ED=4-x,利用勾股定理列方程:x2=32+(4-x)2,求出x的值,再利用勾股定理计算OE的长,由全等证明OE=OF,从而得出EF=2OE.
解答 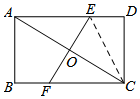 解:连接EC,设AE=x,则ED=4-x,
解:连接EC,设AE=x,则ED=4-x,
∵EF是AC的中垂线,
∴EC=AE=x,
在Rt△EDC中,x2=32+(4-x)2,
x=$\frac{25}{8}$,
∴AE=CE=$\frac{25}{8}$,
∵四边形ABCD是矩形,
∴∠ADC=90°,
在Rt△ADC中,AC=5,
∴OC=AO=$\frac{5}{2}$,
在Rt△EOC中,EO=$\sqrt{E{C}^{2}-O{C}^{2}}$=$\sqrt{(\frac{25}{8})^{2}-(\frac{5}{2})^{2}}$=$\frac{15}{8}$,
∵AD∥BC,
∴∠DAC=∠ACB,
在△AOE和△COF中,
∵$\left\{\begin{array}{l}{∠DAC=∠ACB}\\{AO=OC}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴EF=2OE=2×$\frac{15}{8}$=$\frac{15}{4}$,
故答案为:$\frac{15}{4}$.
点评 本题考查了矩形的性质、线段垂直平分线的性质、全等三角形的性质和判定、勾股定理,在矩形中,通常设未知数,利用勾股定理列方程可求得线段的长,并熟练掌握矩形的性质.

练习册系列答案
相关题目
5.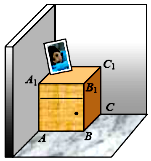 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.当AB=4,BC=4,CC1=5时,则蚂蚁爬过的最短路径的长为$\sqrt{89}$.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.当AB=4,BC=4,CC1=5时,则蚂蚁爬过的最短路径的长为$\sqrt{89}$.
 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.当AB=4,BC=4,CC1=5时,则蚂蚁爬过的最短路径的长为$\sqrt{89}$.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.当AB=4,BC=4,CC1=5时,则蚂蚁爬过的最短路径的长为$\sqrt{89}$.
7.把点(2,-3)先向右平移3个单位长度,再向上平移2个单位长度得到的点的坐标是( )
| A. | (5,-1) | B. | (-1,-5) | C. | (5,-5) | D. | (-1,-1) |
 如图,是某校三个年级学生人数分布扇形统计图,则八年级学生人数所占扇形的圆心角的度数为90°.
如图,是某校三个年级学生人数分布扇形统计图,则八年级学生人数所占扇形的圆心角的度数为90°.