题目内容
2.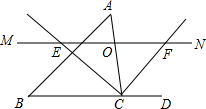 如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠ACB的外角平分线CF于点F,交∠ACB内角平分线CE于E.
如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠ACB的外角平分线CF于点F,交∠ACB内角平分线CE于E.(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论;
(3)在(2)的条件下,试猜想当△ABC满足什么条件时使四边形AECF是正方形,请直接写出你的结论.
分析 (1)根据CE平分∠ACB,MN∥BC,找到相等的角,即∠OEC=∠ECB,再根据等边对等角得OE=OC,同理OC=OF,可得EO=FO.
(2)利用矩形的判定解答,即有一个内角是直角的平行四边形是矩形.
(3)利用已知条件及正方形的判定方法解答.
解答 解:(1)如图1中,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠OEC=∠ECB,
∴∠OEC=∠OCE,
∴OE=OC,
同理,OC=OF,
∴OE=OF.
(2)结论:当点O运动到AC中点处时,四边形AECF是矩形.
理由:如图2中,
如图AO=CO,EO=FO,
∴四边形AECF为平行四边形,
∵CE平分∠ACB,
∴∠ACE=$\frac{1}{2}$∠ACB,
同理,∠ACF=$\frac{1}{2}$∠ACG,
∴∠ECF=∠ACE+∠ACF=$\frac{1}{2}$(∠ACB+∠ACG)=$\frac{1}{2}$×180°=90°,
∴四边形AECF是矩形.
(3)结论:当∠ACB=90°时,四边形AECF是正方形
理由:∵∠BCA=90°,
∵MN∥BC,
∴∠BCA=∠AOM=90°,
∴AC⊥EF,
∴四边形AECF是正方形..
点评 本题考查正方形的判定和性质、矩形的判定和性质、角平分线的定义、平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,记住各种特殊四边形的性质和判定方法,属于中考常考题型.

练习册系列答案
相关题目
14.在一次游戏当中,小明将下面四张扑克牌中的三张旋转了180°,得到的图案和原来的一模一样,小芳看了后,很快知道没有旋转那张扑克牌是( )
| A. |  黑桃Q | B. |  梅花2 | C. |  梅花6 | D. |  方块9 |
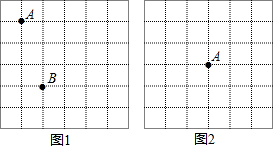
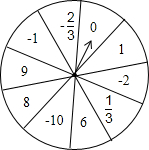 如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少?
如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少?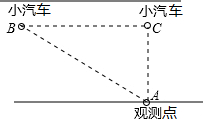 《中华人民共和国道路交通管理条例》规定:小汽车在城市街道上的行驶速度不得超过70千米/时,如图,一辆小汽车在某城市街道直道上行驶,某一时刻刚好行驶到路对面车速检测仪A(观测点)正前方30米处的C处,过了2秒钟后,测得小汽车与车速检测仪间的距离为50米,问:这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)
《中华人民共和国道路交通管理条例》规定:小汽车在城市街道上的行驶速度不得超过70千米/时,如图,一辆小汽车在某城市街道直道上行驶,某一时刻刚好行驶到路对面车速检测仪A(观测点)正前方30米处的C处,过了2秒钟后,测得小汽车与车速检测仪间的距离为50米,问:这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)