题目内容
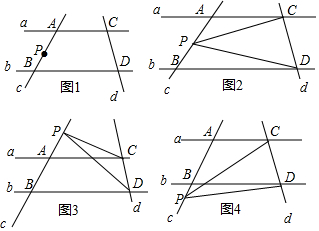
18.【探究活动】如图1:已知直线a与b平行,直线c与直线a、b分别相交于点A、B,直线d与直线a、b分别相交于点C、D,点P在直线c上移动,连接PC、PD.探究∠CPD、∠PCA、∠PDB之间的数量关系.
【探究过程】
(1)当点P在点A、B之间移动时,如图2,写出∠CPD、∠PCA、∠PDB之间的关系,并说明理由.
(2)当点P在A、B两点外移动时,如图3,写出∠CPD、∠PCA、∠PDB之间的关系,并说明理由.
(3)当点P在A、B两点外移动时,如图4,直接写出∠CPD、∠PCA、∠PDB之间的关系.
分析 (1)过P点作PE∥AC交CD于E点,由于AC∥BD,则PE∥BD,根据平行线的性质得∠CPE=∠PCA,∠DPE=∠PDB,据此可得∠CPD、∠PCA、∠PDB之间的关系;
(2)同样,过P点作PE∥AC交CD于E点,由于AC∥BD,则PE∥BD,根据平行线的性质得∠CPE=∠PCA,∠DPE=∠PDB,据此可得∠CPD、∠PCA、∠PDB之间的关系;
(3)运用(2)中的方法,过P点作PE∥AC交CD于E点,由于AC∥BD,则PE∥BD,根据平行线的性质得∠CPE=∠PCA,∠DPE=∠PDB,据此可得∠CPD、∠PCA、∠PDB之间的关系.
解答 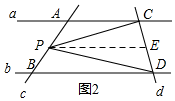 解:(1)∠CPD=∠PCA+∠PDB.
解:(1)∠CPD=∠PCA+∠PDB.
理由:如图2,过P点作PE∥AC交CD于E点,
∵AC∥BD
∴PE∥BD,
∴∠CPE=∠PCA,∠DPE=∠PDB,
∴∠CPD=∠CPE+∠DPE=∠PCA+∠PDB;
(2)∠CPD=∠PDB-∠PCA;
理由:如图3,过P点作PE∥BD交CD于E点,
∵AC∥BD,
∴PE∥AC,
∴∠CPE=∠PCA,∠DPE=∠PDB,
∴∠CPD=∠DPE-∠CPE=∠PDB-∠PCA;
(3)∠CPD=∠PCA-∠PDB.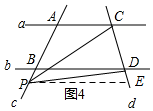
理由如下:如图4,过P点作PF∥BD交CD于E点,
∵AC∥BD,
∴PE∥AC,
∴∠CPE=∠PCA,∠DPE=∠PDB,
∴∠CPD=∠CPE-∠DPE=∠PCA-∠PDB;
点评 本题主要考查了平行线的性质,解决问题的关键是作辅助线构造内错角.解题时注意:两直线平行,内错角相等.

练习册系列答案
相关题目
 如图,E,F,G,H分别是边BD、BC、AC、AD的中点,且AB=CD=6,现有下列结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④四边形EFGH的周长是12.其中正确的是①③④.(把所有正确结论的序号都选上)
如图,E,F,G,H分别是边BD、BC、AC、AD的中点,且AB=CD=6,现有下列结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④四边形EFGH的周长是12.其中正确的是①③④.(把所有正确结论的序号都选上)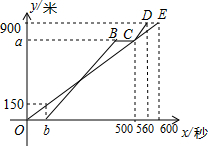 甲、乙两人从学校出发,沿相同的路线分别以不同的速度匀速跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象.
甲、乙两人从学校出发,沿相同的路线分别以不同的速度匀速跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象. AB∥CD,MF⊥NF,MF交AB于点E,NF交CD于点G,∠1=140°,则∠2=50度.
AB∥CD,MF⊥NF,MF交AB于点E,NF交CD于点G,∠1=140°,则∠2=50度.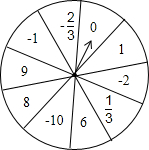 如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少?
如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少? 如图,是某校三个年级学生人数分布扇形统计图,则八年级学生人数所占扇形的圆心角的度数为90°.
如图,是某校三个年级学生人数分布扇形统计图,则八年级学生人数所占扇形的圆心角的度数为90°.