题目内容
14. 如图,A(1,0),B(3,0),C(0,3),D(2,-1),
如图,A(1,0),B(3,0),C(0,3),D(2,-1),(1)试在y轴上找一点P,使三角形ADP的面积与三角形ABC的面积相等.
(2)如果第二象限内有一点Q(a,1),使S△QAC=S△ABC,求Q点坐标.
分析 (1)①如图当P1(0,m)在x的正半轴上时,作DM⊥OB,P1M⊥OP1,根据${S}_{△{P}_{2}AD}$=${S}_{△{P}_{2}OD}{+S}_{△OAD}{-S}_{△AO{P}_{2}}$=S△ABC列出方程求出m,②当P2(0,n)在负半轴上时,根据${S}_{△{P}_{2}AD}$=${S}_{△{P}_{2}OD}{+S}_{△OAD}{-S}_{△AO{P}_{2}}$=S△ABC列出方程解决.
(2)设Q(a,1),(a<0),根据SQAC=S△QOC+S△AOC-S△AOQ=S△ABC列出方程解决.
解答 解:(1)如图1中,当P1在x的正半轴上时,作DM⊥OB,P1M⊥OP1于M,设P10,m),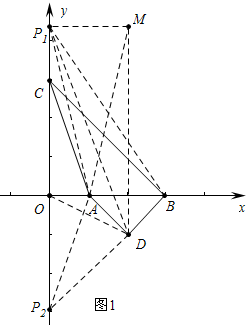
∵${S}_{△{P}_{1}AD}$=${S}_{△{P}_{1}AM}{+S}_{△AMD}$-${S}_{△{P}_{1}DM}$=S△ABC,
∴$\frac{1}{2}$×2×m+$\frac{1}{2}$×(m+1)×1-$\frac{1}{2}$×2×(m+1)=3,
∴m=7.
∴P1(0,7),
当P2(0,n)在负半轴上时,
∵${S}_{△{P}_{2}AD}$=${S}_{△{P}_{2}OD}{+S}_{△OAD}{-S}_{△AO{P}_{2}}$=S△ABC,
∴$\frac{1}{2}$×(-n)×2+$\frac{1}{2}×1×1$-$\frac{1}{2}$×(-n)×1=3,
∴n=-5,
∴P2(0,-5).
∴点P的坐标为(0,7)或(0,-5).
(2)如图2中,设Q(a,1),(a<0),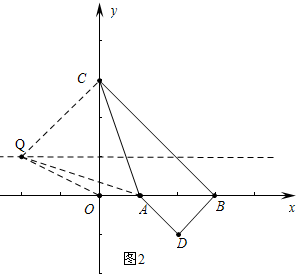
∵SQAC=S△QOC+S△AOC-S△AOQ=S△ABC,
∴$\frac{1}{2}$×3×(-a)+$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×1=3,
∴a=-$\frac{4}{3}$,
∴点Q(-$\frac{4}{3}$,1).
点评 本题考查坐标与性质、三角形的面积等知识,解题的关键是利用分割法找出等量关系列方程解决,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案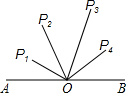 如图,O为线段AB的中点,AB=4cm,P1、P2、P3、P4到点O的距离分别是1cm、2cm、2.8cm、1.7cm,下列四点中能与A、B构成直角三角形的顶点是( )
如图,O为线段AB的中点,AB=4cm,P1、P2、P3、P4到点O的距离分别是1cm、2cm、2.8cm、1.7cm,下列四点中能与A、B构成直角三角形的顶点是( )| A. | P1 | B. | P2 | C. | P3 | D. | P4 |
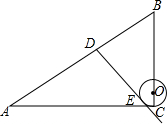 如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,点O为BC上的点,⊙O的半径OC=1,点D是AB边上的动点,过点D作⊙O的一条切线DE(点E为切点),则线段DE的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,点O为BC上的点,⊙O的半径OC=1,点D是AB边上的动点,过点D作⊙O的一条切线DE(点E为切点),则线段DE的最小值为( )| A. | $3\sqrt{2}-1$ | B. | $\sqrt{15}-1$ | C. | $\sqrt{15}$ | D. | 4 |
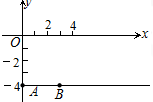 如图,已知A(0,-4)、B(3,-4),C为第四象限内一点且∠AOC=70°,若∠CAB=20°,则∠OCA=40°.
如图,已知A(0,-4)、B(3,-4),C为第四象限内一点且∠AOC=70°,若∠CAB=20°,则∠OCA=40°.