题目内容

4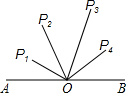．如图，O为线段AB的中点，AB=4cm，P1、P2、P3、P4到点O的距离分别是1cm、2cm、2.8cm、1.7cm，下列四点中能与A、B构成直角三角形的顶点是（　　）
A．P1B．P2C．P3D．P4

分析 根据O为线段AB的中点，AB=4cm，得到AO=BO=2cm，由P1、P2、P3、P4到点O的距离分别是1cm、2cm、2.8cm、1.7cm，得到OP2=2cm，推出OP2=$\frac{1}{2}$AB，根据直角三角形的判定即可得到结论．

解答 解：∵O为线段AB的中点，AB=4cm，
∴AO=BO=2cm，
∵P1、P2、P3、P4到点O的距离分别是1cm、2cm、2.8cm、1.7cm，
∴OP2=2cm，
∴OP2=$\frac{1}{2}$AB，
∴P1、P2、P3、P4四点中能与A、B构成直角三角形的顶点是P2，
故选B．

点评 本题考查了直角三角形的判定定理，熟记直角三角形的判定是解题的关键．

练习册系列答案
相关题目
14．已知成都市某中学八年级三班部分同学的身高为（单位：厘米）：145、162、150、165、165、158，则这组数据的极差为20．
15．如果x2+xy=3，y2+xy=-2，那么x2+3xy+2y2=（　　）
A．-1B．1C．2D．3
12．一个多边形从一个顶点出发的对角线将它分成6个三角形，则这个多边形的边数是8．
19．重庆某汽车制造厂开发了一款新式电动汽车，计划一年生产安装240辆，由于抽调不出足够的熟练工来完成新式电动汽车的安装，工厂决定招聘一些新工人：他们经过培训后上岗，也能独立进行电动汽车的安装，生产开始后，调研部门发现：1名熟练工和2名新工人每月可安装8辆电动汽车；2名熟练工和3名新工人每月可安装14辆电动汽车（假设每名熟练工人的工作效率相同，每名新工人的工作效率也相同）．
（1）求每名熟练工人和每名新工人每月分别可以安装多少辆电动汽车？
（2）如果工厂招聘n（0＜n＜10）名新工人，使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务，那么工厂有哪几种新工人的招聘方案？
（3）在（2）的条件下，工厂个安装电动汽车的每名熟练工每月发2000元的工资，给每名新工人每月发1200元的工资，那么工厂应招聘多少名新工人，使新工人的数量多于熟练工，同时工厂每月支出的工资总额（用W表示，单位：元）尽可能的少？
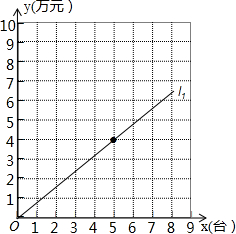9．某专营商场销售一种品牌电脑，每台电脑的进货价是0.4万元．图中的直线l1表示该品牌电脑一天的销售收入y1（万元）与销售量x（台）的关系，已知商场每天的房租、水电、工资等固定支出为3万元．
（1）直线l1对应的函数表达式是y=0.8x，每台电脑的销售价是0.8万元；
（2）写出商场一天的总成本y2（万元）与销售量x（台）之间的函数表达式：y2=0.4x+3；
（3）在图的直角坐标系中画出第（2）小题的图象（标上l2）；
（4）通过计算说明：每天销售量达到多少台时，商场可以盈利．
16．某打印社打印材料的收费标准为：每份材料收0.2元的印刷费，并收10元的制版费．
（1）求打字社打印材料的收费y（元）与印刷数量x（份）间的函数表达式；
（2）求印刷50份材料收费多少元？
13．如图，二次函数y=x2+2x+c的图象与x轴交于点A和点B（1，0），以AB为边在x轴上方作正方形ABCD，动点P从点A出发，以每秒2个单位长度的速度沿x轴的正方向匀速运动，同时动点Q从点C出发，以每秒1个单位长度的速度沿CB匀速运动，当点Q到达终点B时，点P停止运动，设运动时间为t秒．连接DP，过点P作DP的垂线与y轴交于点E．
（1）求二次函数的解析式及点A的坐标；
（2）当点P在线段AO（点P不与A、O重合）上运动至何处时，线段OE的长有最大值，并求出这个最大值；
（3）在P，Q运动过程中，求当△DPE与以D，C，Q为顶点的三角形相似时t的值；
（4）是否存在t，使△DCQ沿DQ翻折得到△DC′Q，点C′恰好落在抛物线的对称轴上？若存在，请求出t的值；若不存在，请说明理由．
14．如图，A（1，0），B（3，0），C（0，3），D（2，-1），
（1）试在y轴上找一点P，使三角形ADP的面积与三角形ABC的面积相等．
（2）如果第二象限内有一点Q（a，1），使S△QAC=S△ABC，求Q点坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网