题目内容
12.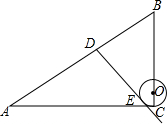 如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,点O为BC上的点,⊙O的半径OC=1,点D是AB边上的动点,过点D作⊙O的一条切线DE(点E为切点),则线段DE的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,点O为BC上的点,⊙O的半径OC=1,点D是AB边上的动点,过点D作⊙O的一条切线DE(点E为切点),则线段DE的最小值为( )| A. | $3\sqrt{2}-1$ | B. | $\sqrt{15}-1$ | C. | $\sqrt{15}$ | D. | 4 |
分析 连接OE、OD,由DE为⊙O的切线知DE2+OE2=OD2即DE=$\sqrt{O{D}^{2}-1}$,要使DE最小,则OD最小即可,根据题意可知当OD⊥AB时,OD最小,通过证明△BDO∽△BCA可得OD的长度,可得DE的最小值.
解答 解:如图,连接OE、OD,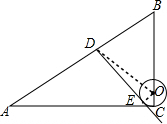
在Rt△ABC中,∵∠C=90°,AC=8,AB=10,
∴BC=6,
∵DE为⊙O的切线,
∴∠DEO=90°,
∴DE2+OE2=OD2,
∵OE=1,
∴DE2=OD2-1,即DE=$\sqrt{O{D}^{2}-1}$,
要使DE最小,则OD最小即可,
∵D为AB边上的动点,
∴当OD⊥AB时,OD最小,
∵BC=6,OC=1,
∴BO=5,
∵∠ODB=∠ACB=90°,∠B=∠B,
∴△BDO∽△BCA,
∴$\frac{OD}{AC}=\frac{BO}{AB}$,即$\frac{OD}{8}=\frac{5}{10}$,
解得:OD=4,
∴DE=$\sqrt{{4}^{2}-1}$=$\sqrt{15}$,
故选:C.
点评 本题主要考查切线的性质,关于圆的切线常添的辅助线是连接圆心和切点可得直角,本题中意识到要使DE最小则OD最小即可是关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 如图,A(1,0),B(3,0),C(0,3),D(2,-1),
如图,A(1,0),B(3,0),C(0,3),D(2,-1), 如图,△ABC内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论;
如图,△ABC内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论; 如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°. 如图,AB=16cm,点D为射线AC上一点,且AD=20cm,点E是平面上任一点,且BE=3AE.
如图,AB=16cm,点D为射线AC上一点,且AD=20cm,点E是平面上任一点,且BE=3AE. 如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD,若AB=4,AD=6,∠ABC=60°,PD的长2$\sqrt{7}$,四边形ABEF的面积8$\sqrt{3}$.
如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD,若AB=4,AD=6,∠ABC=60°,PD的长2$\sqrt{7}$,四边形ABEF的面积8$\sqrt{3}$. 如图,点D、E分别是等边三角形ABC的两边AB、AC上的点,且∠BOD=60°,求证:AD=CE.
如图,点D、E分别是等边三角形ABC的两边AB、AC上的点,且∠BOD=60°,求证:AD=CE. 如图,已知∠BDA=45°,BD=4,AD=3,且三角形ABC是等腰直角三角形,则CD=$\sqrt{34}$.
如图,已知∠BDA=45°,BD=4,AD=3,且三角形ABC是等腰直角三角形,则CD=$\sqrt{34}$.