题目内容
5.先化简,再求值:($\frac{a+2}{{a}^{2}-2a}$$-\frac{a-1}{{a}^{2}-4a+4}$)$÷\frac{4-a}{a}$,其中a=$\frac{1}{2}$.分析 先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
解答 解:原式=[$\frac{a+2}{a(a-2)}$-$\frac{a-1}{(a-2)^{2}}$]•$\frac{a}{4-a}$
=$\frac{(a+2)(a-2)-a(a-1)}{{a(a-2)}^{2}}$•$\frac{a}{4-a}$
=$\frac{{a}^{2}-4-{a}^{2}+a}{{a(a-2)}^{2}}$•$\frac{a}{4-a}$
=$\frac{a-4}{{a(a-2)}^{2}}$•$\frac{a}{4-a}$
=-$\frac{1}{(a-2)^{2}}$,
当a=$\frac{1}{2}$时,原式=-$\frac{1}{{(\frac{1}{2}-2)}^{2}}$=-$\frac{4}{9}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
15.如果x2+xy=3,y2+xy=-2,那么x2+3xy+2y2=( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
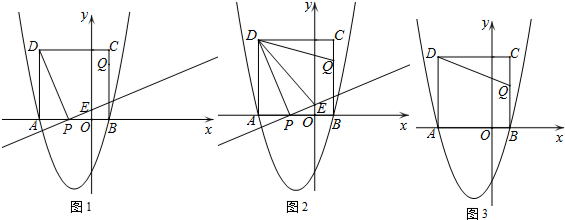
 如图,A(1,0),B(3,0),C(0,3),D(2,-1),
如图,A(1,0),B(3,0),C(0,3),D(2,-1),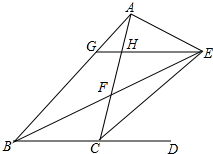 如图,△ABC内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论;
如图,△ABC内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论;