题目内容
2.解下列方程:(1)10(x-1)=5.
(2)5x+2=7x-8
(3)$\frac{7x-3}{2}$-$\frac{4x+1}{5}$=1.
分析 (1)方程去括号,移项合并,把x系数化为1,即可求出解;
(2)方程移项合并,把x系数化为1,即可求出解;
(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)去括号得:10x-10=5,
移项合并得:10x=15,
解得:x=1.5;
(2)移项合并得:-2x=-10,
解得:x=5;
(3)去分母得:5(7x-3)-2(4x+1)=10,
去括号得:35x-15-8x-2=10,
移项合并得:27x=27,
解得:x=1.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
相关题目
12. 如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )
如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )
 如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )
如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}+1}{4}$ |
17.已知a,b是一元二次方程x2-2x-1=0的两个实数根,则代数式(a-b)(a+b-2)+ab的值等于( )
| A. | -1 | B. | 1 | C. | ±8$\sqrt{2}$-1 | D. | ±8$\sqrt{2}$+1 |
7. 下图是某中学的平面示意图,每个正方形格子的边长为1,如果校门所在位置的坐标为(2,4),小明所在位置的坐标为(-6,-1),那么坐标(3,-2)在示意图中表示的是( )
下图是某中学的平面示意图,每个正方形格子的边长为1,如果校门所在位置的坐标为(2,4),小明所在位置的坐标为(-6,-1),那么坐标(3,-2)在示意图中表示的是( )
 下图是某中学的平面示意图,每个正方形格子的边长为1,如果校门所在位置的坐标为(2,4),小明所在位置的坐标为(-6,-1),那么坐标(3,-2)在示意图中表示的是( )
下图是某中学的平面示意图,每个正方形格子的边长为1,如果校门所在位置的坐标为(2,4),小明所在位置的坐标为(-6,-1),那么坐标(3,-2)在示意图中表示的是( )| A. | 图书馆 | B. | 教学楼 | C. | 实验楼 | D. | 食堂 |
14. 如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )
如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )
 如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )
如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )| A. | 90° | B. | 100° | C. | 110° | D. | 120° |
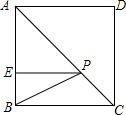 如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是2$\sqrt{34}$cm.
如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是2$\sqrt{34}$cm.