题目内容
1.若一次函数y=-x+b-$\frac{3}{2}$的图象不过第三象限,则b的取值范围是b≥$\frac{3}{2}$.分析 根据一次函数的图象不经过第三象限列出关于b的不等式,求出b的取值范围即可.
解答 解:∵一次函数y=-x+b-$\frac{3}{2}$的图象不过第三象限,
∴b-$\frac{3}{2}$≥0,解得b≥$\frac{3}{2}$.
故答案为:b≥$\frac{3}{2}$.
点评 本题考查的是一次函数的性质,熟知一次函数y=kx+b(k≠0)中,当k<0,b>0时,函数图象经过一二四象限是解答此题的关键.

练习册系列答案
相关题目
12. 如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )
如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )
 如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )
如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}+1}{4}$ |
9.函数y=-x2+2x+$\frac{1}{2}$有最值为( )
| A. | 最大值$\frac{3}{2}$ | B. | 最小值$\frac{3}{2}$ | C. | 最大值-$\frac{1}{2}$ | D. | 最小值-$\frac{1}{2}$ |
16.如果$\frac{6sinα-2cosα}{2sinα+cosα}$=2,那么tanα=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |
 如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线y=x于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点B4的纵坐标为2$\sqrt{2}$.
如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线y=x于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点B4的纵坐标为2$\sqrt{2}$.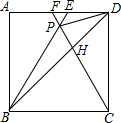 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
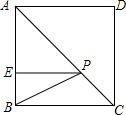 如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是2$\sqrt{34}$cm.
如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是2$\sqrt{34}$cm.