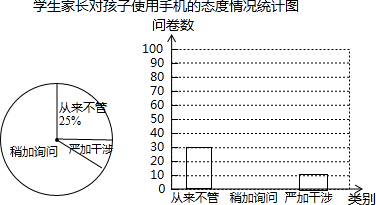
解不等式组:$\left\{\begin{array}{l}{\frac{1}{2}x+3≥-1}\\{x-2(x-3)＞0}\end{array}\right.$．题目和参考答案——青夏教育精英家教网—

题目内容

20．解不等式组：$\left\{\begin{array}{l}{\frac{1}{2}x+3≥-1}\\{x-2（x-3）＞0}\end{array}\right.$．

分析先求出两个不等式的解集，再求不等式组的公共解．

解答解：$\left\{\begin{array}{l}{\frac{1}{2}x+3≥-1①}\\{x-2（x-3）＞0②}\end{array}\right.$
解不等式①得x≥-8；
解不等式②得x＜6；
所以不等式组的解集为-8≤x＜6．

点评本题考查了解一元一次不等式，要遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．

练习册系列答案

相关题目

2．正比例函数的图象经过点（-1，2），则这个图象必须经过点（　　）

11．某校为了了解学生家长对孩子使用手机的态度情况，随机抽取部分学生家长进行问卷调查，发出问卷140份，每位学生家长1份，每份问卷仅表明一种态度，将回收的问卷进行整理（假设回收的问卷都有效），并绘制了如图两幅不完整的统计图．

根据以上信息解答下列问题：
（1）回收的问卷数为120份，“严加干涉”部分对应扇形的圆心角度数为30°．
（2）把条形统计图补充完整
（3）若将“稍加询问”和“从来不管”视为“管理不严”，已知全校共1500名学生，请估计该校对孩子使用手机“管理不严”的家长大约有多少人？
（4）在这次调查中共有甲、乙、丙、丁四位家长“严加干涉”，现准备从这四位家长中抽取两名家长进行讲座，请用列表法或树状图法求出抽取的两人恰好是甲和乙的概率．

8．

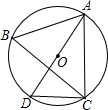如图，⊙O是△ABC的外接圆，AD是⊙O的直径，连接CD，若⊙O的半径r=5，AC=5$\sqrt{3}$，
（1）求CD的长，
（2）求∠B的度数．

15．

如图，直线AB∥CD，∠E=40°，∠1=25°，则∠CAB=（　　）

5．

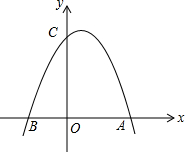如图，已知抛物线经过点A（3，0）、B（-2，0）、C（0，6）．
（1）求抛物线对应的二次函数的表达式；
（2）P是抛物线上的一点，若PB=PC，求出P点的坐标；
（3）在第一象限内的抛物线上是否存在点M，使四边形OAMC的面积最大？若存在，求出M点的坐标，若不存在，请说明理由．

12．

如图是统计一位病人的体温变化图，则这位病人在16时的体温约是（　　）

9．（1）先化简，再求值：（a-2）²+a（a+4），其中a=$\sqrt{3}$；
（2）解不等式组$\left\{\begin{array}{l}{\frac{x+1}{2}≤1}\\{1-2x＜4}\end{array}\right.$，并求出不等式组的非负整数解．

10．

如图，从一个直径是2m的圆形铁皮中剪出一个圆心角为90°的扇形，如果将剪下来的扇形围成一个圆锥，那么圆锥的高等于$\frac{\sqrt{30}}{4}$m．

试题分类