题目内容
10. 如图,从一个直径是2m的圆形铁皮中剪出一个圆心角为90°的扇形,如果将剪下来的扇形围成一个圆锥,那么圆锥的高等于$\frac{\sqrt{30}}{4}$m.
如图,从一个直径是2m的圆形铁皮中剪出一个圆心角为90°的扇形,如果将剪下来的扇形围成一个圆锥,那么圆锥的高等于$\frac{\sqrt{30}}{4}$m.
分析 设圆锥的底面圆半径为r.先根据勾股定理求出扇形ABC的半径,再根据圆锥的弧长等于底面周长列方程求出r,然后利用勾股定理求得圆锥的高即可.
解答 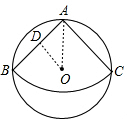 解:设圆锥的底面圆半径为r.
解:设圆锥的底面圆半径为r.
过圆心O作OD⊥AB于点D,连接AO,如图.
∵∠BAC=90°,
∴∠DAO=45°.
∴AD=AO•cos45°=$\frac{\sqrt{2}}{2}$.
则扇形ABC的半径为$\sqrt{2}$.
∵2πr=$\frac{90π×\sqrt{2}}{180}$.
∴r=$\frac{\sqrt{2}}{4}$,
∴圆锥的高为$\sqrt{(\sqrt{2})^{2}-(\frac{\sqrt{2}}{4})^{2}}$=$\frac{\sqrt{30}}{4}$,
故答案为:$\frac{\sqrt{30}}{4}$m.
点评 此题考查了圆锥的计算的知识,应用的知识点为:圆锥的弧长等于底面周长;难点是得到扇形的半径.

练习册系列答案
相关题目
18.下列计算正确的是( )
| A. | a3÷a2=1 | B. | a2+a3=a5 | C. | (a3)2=a5 | D. | a2•a3=a5 |
15.下列运算错误的是( )
| A. | x5•x5=x10 | B. | x5+x5=2x5 | ||
| C. | (-x5)5=-x25 | D. | (2x2y)3÷($\frac{1}{4}$xy3)=$\frac{1}{2}$x5 |
19.分式方程$\frac{2}{x-3}$-$\frac{2x}{3-x}$=10的解是( )
| A. | 3 | B. | 2 | C. | 0 | D. | 4 |