题目内容
8.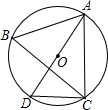 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,(1)求CD的长,
(2)求∠B的度数.
分析 (1)根据勾股定理计算即可;
(2)根据正弦的定义求出∠D,根据圆周角定理解答即可.
解答 解:(1)∵AD是⊙O的直径,
∴∠ACD=90°,
∴CD=$\sqrt{A{D}^{2}-A{C}^{2}}$=5;
(2)sinD=$\frac{AC}{AD}$=$\frac{\sqrt{3}}{2}$,
则∠D=60°,
由圆周角定理得,∠B=∠D=60°.
点评 本题考查的是三角形的外接圆与外心的概念和性质,掌握圆周角定理、勾股定理、特殊角的三角函数值是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17.湖州师院大学生小王利用暑假开展了30天的社会实践活动,参与了湖州浙北超市的经营,了解到某成本为15元/件的商品在x天销售的相关信息,如表表示:
设该超市在第x天销售这种商品获得的利润为y元.
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
| 销售量p(件) | P=45-x |
| 销售单价q(元/件) | 当1≤x≤18时,q=20+x 当18<x≤30时,q=38 |
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
18.下列计算正确的是( )
| A. | a3÷a2=1 | B. | a2+a3=a5 | C. | (a3)2=a5 | D. | a2•a3=a5 |
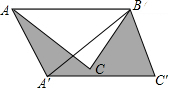 如图,在△ABC中,AB=6cm,∠CAB=45°,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为9$\sqrt{2}$cm2.
如图,在△ABC中,AB=6cm,∠CAB=45°,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为9$\sqrt{2}$cm2.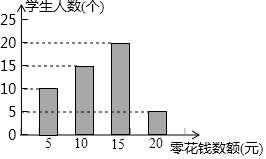 某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示.
某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示.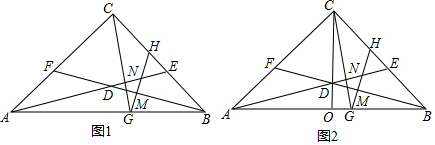
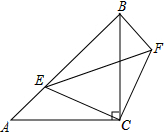 已知:如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上.
已知:如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上.