题目内容
11.某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.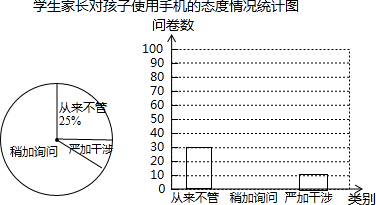
根据以上信息解答下列问题:
(1)回收的问卷数为120份,“严加干涉”部分对应扇形的圆心角度数为30°.
(2)把条形统计图补充完整
(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?
(4)在这次调查中共有甲、乙、丙、丁四位家长“严加干涉”,现准备从这四位家长中抽取两名家长进行讲座,请用列表法或树状图法求出抽取的两人恰好是甲和乙的概率.
分析 (1)用“从来不管”的问卷数除以其所占百分比求出回收的问卷总数;用“严加干涉”部分的问卷数除以问卷总数得出百分比,再乘以360°即可;
(2)用问卷总数减去其他两个部分的问卷数,得到“稍加询问”的问卷数,进而补全条形统计图;
(3)用“稍加询问”和“从来不管”两部分所占的百分比的和乘以1500即可得到结果;
(4)画树状图得出所有等可能的情况数,找出恰好是甲与乙的情况,即可确定出所求概率.
解答 解:(1)回收的问卷数为:30÷25%=120(份),
“严加干涉”部分对应扇形的圆心角度数为:$\frac{10}{120}$×360°=30°.
故答案为:120,30°;
(2)“稍加询问”的问卷数为:120-(30+10)=80(份),
补全条形统计图,如图所示:
(3)根据题意得:1500×$\frac{30+80}{120}$=1375(人),
则估计该校对孩子使用手机“管理不严”的家长大约有1375人;
(4)画树状图,如图所示:
所有等可能的情况有12种,其中恰好是甲与乙的情况有2种,
∴抽取的两人恰好是甲和乙的概率为$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查的是条形统计图和扇形统计图的综合运用,也考查了列表法与树状图法.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了利用样本估计总体.

练习册系列答案
相关题目
 如图,一货船在港口A的正北100 n mi1e的B处,遇到危险后,以25 n mile/h的速度向正东漂行且发出求救信号,一军舰接到求救信号后立即由港口A以50 n mile/h的速度向北偏东方向航行,赶去支援,求军舰航行$\frac{200\sqrt{3}}{3}$n mi1e可追上货船.
如图,一货船在港口A的正北100 n mi1e的B处,遇到危险后,以25 n mile/h的速度向正东漂行且发出求救信号,一军舰接到求救信号后立即由港口A以50 n mile/h的速度向北偏东方向航行,赶去支援,求军舰航行$\frac{200\sqrt{3}}{3}$n mi1e可追上货船.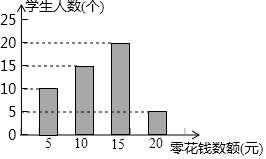 某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示.
某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示.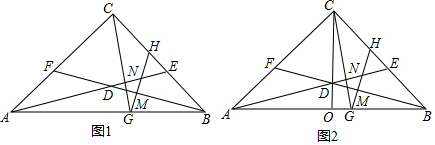
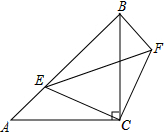 已知:如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上.
已知:如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上.