题目内容
6. 如图,∠ACB=90°,CD⊥AB,AC=5,BC=12,AB=13.点A到CD边的距离是$\frac{25}{13}$;点C到AB边的距离是$\frac{60}{13}$.
如图,∠ACB=90°,CD⊥AB,AC=5,BC=12,AB=13.点A到CD边的距离是$\frac{25}{13}$;点C到AB边的距离是$\frac{60}{13}$.
分析 根据条件分别求出AD、CD的长度即可.
解答 解:由于$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD
∴CD=$\frac{60}{13}$
在Rt△ACD中,
由勾股定理可得:AD=$\frac{25}{13}$
∴A到CD边的距离为:$\frac{25}{13}$,
C在AB边的距离为:$\frac{60}{13}$
故答案为:$\frac{25}{13}$,$\frac{60}{13}$
点评 本题考查点到直线的距离,解题的关键是熟练运用勾股定理,本题属于中等题型.

练习册系列答案
相关题目
18.将三角形、菱形、正方形、圆四种图形(大小不计)组合如图,观察并思考最后一图对应的数为( )


| A. | 13 | B. | 24 | C. | 31 | D. | 42 |
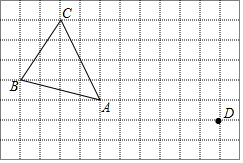 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.