��Ŀ����
1����һ��֪ʶ��������M��N�������ϣ���M��N������ʵ���ֱ���a��b�����߶�MN�ij��ȿɱ�ʾΪ|a-b|��
�������������
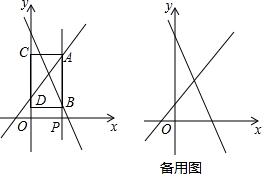
��ͼ����P��m��0����x����������һ���㣬����P��x��Ĵ��ߣ��ֱ�һ�κ���y=x+1��y=-2x+4��ͼ���ڵ�A��B������A��B��y��Ĵ��ߣ�����ֱ�Ϊ��C��D
��1���ú���m��ʽ�ӱ�ʾ�߶�AB�ij��ȣ�
��2�����ı���ABDC�����Ϊ$\frac{3}{4}$����m��ֵ��
���� ��һ��֪ʶ���ӣ��������⼴�ɵõ����ۣ�
������������⣺��1��������֪�����õ�A��m��m+1������m��-2m+4�������ǵõ����ۣ�
��2��������֪�����õ��ı���ABDC�Ǿ��Σ����ݾ��ε�����з��̼��ɵõ����ۣ�
��� �⣺��һ��֪ʶ���ӣ��߶�MN�ij��ȿɱ�ʾΪ|a-b|��
�ʴ�Ϊ��|a-b|��
������������⣺��1����AB��x�ᣬ��P��m��0����
��A��m��m+1������m��-2m+4����
��AB=��m+1��-��-2m+4��=3m-3��
��2����AC��y�ᣬBD��y�ᣬ
��AC��BD����ACD=90�㣬
��AB��x�ᣬ
��AB��CD��
���ı���ABDC�Ǿ��Σ�
��S����ABDC=AB•BD=m��3m-3��=$\frac{3}{4}$����S����ABDC=AB•BD=m��-3m+3��=$\frac{3}{4}$��
��ã�m=$\frac{1+\sqrt{2}}{2}$��m=$\frac{1-\sqrt{2}}{2}$����ȥ������m=$\frac{1}{2}$��
��m��ֵΪ$\frac{1+\sqrt{2}}{2}$��$\frac{1}{2}$��
���� ���⿼������ֱ��ƽ�л��ཻ��ʵ�������ᣬ���ε��ж������ʣ���ȷ��ʶ��ͼ���ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
13��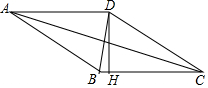 ��ͼ���ı���ABCD�����Σ�AC=8��DB=6��DH��BC��H����DH���ڣ�������
��ͼ���ı���ABCD�����Σ�AC=8��DB=6��DH��BC��H����DH���ڣ�������
 ��ͼ���ı���ABCD�����Σ�AC=8��DB=6��DH��BC��H����DH���ڣ�������
��ͼ���ı���ABCD�����Σ�AC=8��DB=6��DH��BC��H����DH���ڣ�������| A�� | $\frac{24}{5}$ | B�� | $\frac{12}{5}$ | C�� | 5 | D�� | 4 |
10���üӼ����ⷽ����$\left\{\begin{array}{l}{3x-2y=3��}\\{4x+y=15��}\end{array}\right.$ʱ�������ȥy�����ݵķ����ǣ�������
| A�� | �١�4-�ڡ�3 | B�� | �١�4+�ڡ�3 | C�� | �ڡ�2-�� | D�� | �ڡ�2+�� |
11����������������������ǣ�������
| A�� | �Զ������ | B�� | �ڴ������ | C�� | ͬ���ڽǻ��� | D�� | ͬλ����� |

 ��ͼ����ACB=90�㣬CD��AB��AC=5��BC=12��AB=13����A��CD�ߵľ�����$\frac{25}{13}$����C��AB�ߵľ�����$\frac{60}{13}$��
��ͼ����ACB=90�㣬CD��AB��AC=5��BC=12��AB=13����A��CD�ߵľ�����$\frac{25}{13}$����C��AB�ߵľ�����$\frac{60}{13}$��