题目内容
14.在下列方程:①7x2-12x+5=0;②6x2-13x-5=0;③4x2+21x+5=0;④2x2+15x-5=0中,两根均为负数的方程是③(填序号)分析 因为两根均为负数,所以两实数根的和小于零,两根之积大于零.解题时检验两根之和-$\frac{b}{a}$是否小于零及两根之积$\frac{c}{a}$是否大于零.
解答 解:①x1x2=$\frac{5}{7}$>0,x1+x2=$\frac{12}{7}$>0,两根均为正数;
②x1x2=-$\frac{5}{6}$<0,x1+x2=$\frac{13}{6}$>0,两根为一正一负;
③x1x2=$\frac{5}{4}$>0,x1+x2=-$\frac{21}{4}$<0,两根均为负数;
④x1x2=-$\frac{5}{2}$<0,x1+x2=-$\frac{15}{2}$<0,两根为一正一负.
故答案为:③.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
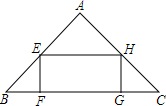 如图,在一个直角边长为4cm的等腰直角三角形内部,截出一个矩形EFGH,设EF的长为x cm,矩形的面积为y cm2.
如图,在一个直角边长为4cm的等腰直角三角形内部,截出一个矩形EFGH,设EF的长为x cm,矩形的面积为y cm2. 已知线段a(如图),把它分成1:2:3三段.
已知线段a(如图),把它分成1:2:3三段. 如图,AE=AC=AD,BD=BA,CB=CE,求∠ABD的度数.
如图,AE=AC=AD,BD=BA,CB=CE,求∠ABD的度数.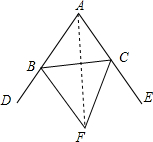 如图,△ABC的外角∠CBD,∠BCE的平分线相交于点F,求证:
如图,△ABC的外角∠CBD,∠BCE的平分线相交于点F,求证: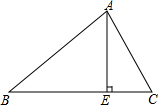 已知△ABC的面积为10cm2,其中BC为x(cm),BC边上的高线长AE为y(cm).
已知△ABC的面积为10cm2,其中BC为x(cm),BC边上的高线长AE为y(cm).