题目内容
5.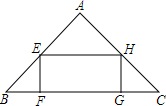 如图,在一个直角边长为4cm的等腰直角三角形内部,截出一个矩形EFGH,设EF的长为x cm,矩形的面积为y cm2.
如图,在一个直角边长为4cm的等腰直角三角形内部,截出一个矩形EFGH,设EF的长为x cm,矩形的面积为y cm2.(1)写出y与x之间的函数关系式;
(2)当x取何值时,y最大?最大值是多少?
分析 (1)根据已知条件可知△AEH∽△ABC,从而可以用含x的代数式表示EH,利用矩形面积公式可得y与x之间的函数关系式;
(2)根据公式法,结合已求得的二次函数解析式可解.
解答 解:(1)如图所示,过点A作AD⊥BC,垂足为D.
在Rt△ABC中,AB=AC=4,
由勾股定理得:BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
∵AD⊥BC,
∴△ABD为等腰直角三角形.
∴AD=BD═2$\sqrt{2}$.
∵四边形EFGH是矩形,
∴EH∥BC,
∴△AEH∽△ABC.
∴$\frac{EH}{BC}=\frac{AD-EF}{AD}$,即$\frac{EH}{4\sqrt{2}}$=$\frac{2\sqrt{2}-x}{2\sqrt{2}}$.
∴EH=-2x+4$\sqrt{2}$.
∴y=x(-2x+4$\sqrt{2}$)=-2x2+4$\sqrt{2}$x;
(2)∵a=-2<0,
∴二次函数y=-2x2+4$\sqrt{2}$x有最大值,
当x=$-\frac{b}{2a}$=$-\frac{4\sqrt{2}}{-2×2}$=$\sqrt{2}$时,
y最大值=$\frac{4ac-{b}^{2}}{4a}$=$\frac{-2×4×0-(4\sqrt{2})^{2}}{-2×4}$=4.
点评 本题主要考查的是二次函数的解析式、二次函数的最值、相似三角形的性质、矩形的性质,利用相似三角形的性质求得矩形的长(用含x式子表示)是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知点A、B,且AB>4,画经过A、B两点且半径为2的圆有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
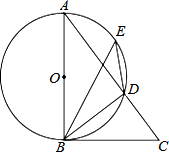 如图,AB是⊙O的直径,点E是$\widehat{AD}$上的一点,∠DBC=∠BED.
如图,AB是⊙O的直径,点E是$\widehat{AD}$上的一点,∠DBC=∠BED.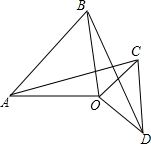 如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=90°,当将△COD绕点O顺时针旋转时,连线AC与BD之间的大小关系如何?试猜想并证明你的结论.
如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=90°,当将△COD绕点O顺时针旋转时,连线AC与BD之间的大小关系如何?试猜想并证明你的结论.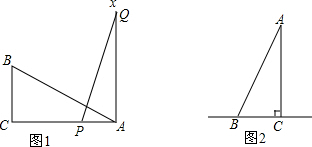
 如图,△ABC中,∠1=∠2,∠ABC=∠C,∠4=∠5,求∠5的度数.
如图,△ABC中,∠1=∠2,∠ABC=∠C,∠4=∠5,求∠5的度数.