题目内容
 如图,已知一次函数y1=x-6与反比例函数y2=
如图,已知一次函数y1=x-6与反比例函数y2=| 7 |
| x |
(1)求A、B两点的坐标;
(2)如果y1-y2>0,求x的取值范围;
(3)如果y1+y2>0,求x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)首先联立一次函数与反比例函数的解析式可得
,继而求得A、B两点的坐标;
(2)由如果y1-y2>0,可得y1>y2,结合图象,即可求得答案;
(3)由y1+y2>0,可得即x-6>-
,然后设y3=-
,求得y1与y3的交点坐标,结合图象即可求得答案.
|
(2)由如果y1-y2>0,可得y1>y2,结合图象,即可求得答案;
(3)由y1+y2>0,可得即x-6>-
| 7 |
| x |
| 7 |
| x |
解答: 解:(1)联立得:
解:(1)联立得:
,
解得:
或
,
∴A(7,1),B(-1,-7);
(2)如图:如果y1-y2>0,则x的取值范围为:-1<x<0或x>7;
(3)如果y1+y2>0,则x-6+
>0,
即x-6>-
,
设y3=-
,
则y1与y3的交点坐标为:(3-
,-3-
),(3+
,-3+
),
∴x的取值范围为:0<x<3-
或x>3+
.
 解:(1)联立得:
解:(1)联立得:
|
解得:
|
|
∴A(7,1),B(-1,-7);
(2)如图:如果y1-y2>0,则x的取值范围为:-1<x<0或x>7;
(3)如果y1+y2>0,则x-6+
| 7 |
| x |
即x-6>-
| 7 |
| x |
设y3=-
| 7 |
| x |
则y1与y3的交点坐标为:(3-
| 2 |
| 2 |
| 2 |
| 2 |
∴x的取值范围为:0<x<3-
| 2 |
| 2 |
点评:此题考查了一次函数与反比例函数的交点问题.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目

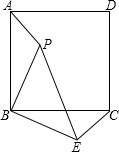 已知:点P是正方形内一点,△ABP旋转后能与△CBE重合.
已知:点P是正方形内一点,△ABP旋转后能与△CBE重合. 如图,△ABC中,∠B,∠C的平分线相交于点O,过O作DE∥BC,若BD+EC=5,则DE等于多少?
如图,△ABC中,∠B,∠C的平分线相交于点O,过O作DE∥BC,若BD+EC=5,则DE等于多少? 如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足
如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足 如图,△ABC为等腰三角形,AB=AC,BD为角平分线,延长BC到E,使CE=CD,作DH⊥BE,垂足为H.
如图,△ABC为等腰三角形,AB=AC,BD为角平分线,延长BC到E,使CE=CD,作DH⊥BE,垂足为H.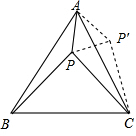 如图,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=
如图,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=