题目内容
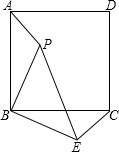 已知:点P是正方形内一点,△ABP旋转后能与△CBE重合.
已知:点P是正方形内一点,△ABP旋转后能与△CBE重合.(1)△ABP旋转的旋转中心是什么?旋转了多少度?
(2)若BP=2,求PE的长.
考点:旋转的性质,勾股定理,正方形的性质
专题:计算题
分析:(1)根据正方形的性质得BA=BC,∠ABC=90°,然后根据旋转的性质求解;
(2)根据旋转的性质得BP=BE=2,∠PBE=90°,然后根据等腰直角三角形的性质求解.
(2)根据旋转的性质得BP=BE=2,∠PBE=90°,然后根据等腰直角三角形的性质求解.
解答:解:(1)∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
∵△ABP旋转后能与△CBE重合,
∴△ABP旋转的旋转中心是点B,按顺时针方向旋转90°;
(2)∵△ABP旋转后能与△CBE重合,
∴BP=BE=2,∠PBE=90°,
∴PE=
PB=2
.
答:(1)△ABP旋转的旋转中心是点B,按顺时针方向旋转90°;(2)PE为2
.
∴BA=BC,∠ABC=90°,
∵△ABP旋转后能与△CBE重合,
∴△ABP旋转的旋转中心是点B,按顺时针方向旋转90°;
(2)∵△ABP旋转后能与△CBE重合,
∴BP=BE=2,∠PBE=90°,
∴PE=
| 2 |
| 2 |
答:(1)△ABP旋转的旋转中心是点B,按顺时针方向旋转90°;(2)PE为2
| 2 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
相关题目
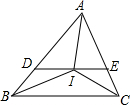 如图,△ABC中,IB,IC分别平分∠ABC,∠ACB,过I点作DE∥BC,分别交AB于D,交AC于E,给出下列结论:
如图,△ABC中,IB,IC分别平分∠ABC,∠ACB,过I点作DE∥BC,分别交AB于D,交AC于E,给出下列结论: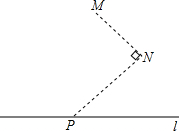 如图所示,在水渠l的同一侧有两个水池M与N,把水渠水先引到水池N,再由N引人水池M.连接MN,作∠MNP=90°,NP交l于点P,将水渠水由P放到N,再由N放到M,所行路径最短,对吗?如果不对,你是怎样设计的?写出你的设计方案.
如图所示,在水渠l的同一侧有两个水池M与N,把水渠水先引到水池N,再由N引人水池M.连接MN,作∠MNP=90°,NP交l于点P,将水渠水由P放到N,再由N放到M,所行路径最短,对吗?如果不对,你是怎样设计的?写出你的设计方案. 如图,在平面直角坐标中,矩形OABC的顶点O为坐标原点,OA在x轴上,OC在y轴上,点B的坐标为(-3,4),反比例函数
如图,在平面直角坐标中,矩形OABC的顶点O为坐标原点,OA在x轴上,OC在y轴上,点B的坐标为(-3,4),反比例函数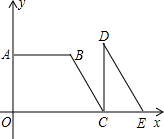 四边形OABC是直角梯形,△CDE是直角三角形,点A在y轴上,点C、E在x轴上,BC∥DE,抛物线y=-
四边形OABC是直角梯形,△CDE是直角三角形,点A在y轴上,点C、E在x轴上,BC∥DE,抛物线y=- 如图,已知一次函数y1=x-6与反比例函数y2=
如图,已知一次函数y1=x-6与反比例函数y2=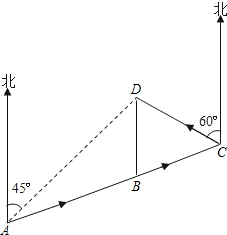 如图,要环绕A、B、C、D四地修筑一条高等级公路ABCDA.已知A、B、C三地在同一直线上,D地在A地的北偏东45°方向,在B地的正北方向,在C地北偏西60°方向,C地在A地的北偏东75°方向,B、D两地相距10km.如果该公路每公里造价为2000万元,求该公路全长的造价是多少万元?(用根号表示)
如图,要环绕A、B、C、D四地修筑一条高等级公路ABCDA.已知A、B、C三地在同一直线上,D地在A地的北偏东45°方向,在B地的正北方向,在C地北偏西60°方向,C地在A地的北偏东75°方向,B、D两地相距10km.如果该公路每公里造价为2000万元,求该公路全长的造价是多少万元?(用根号表示)