题目内容
在Rt△ABC中,∠C为直角,AC=6,∠BAC的角平分线AD=4
,解此直角三角形.
| 3 |
考点:解直角三角形
专题:
分析:先在Rt△ADC中求出AD的长和∠CAD的度数,再利用三角函数求出AB的长,最后求出∠B的度数.
解答: 解:在Rt△ADC中,
解:在Rt△ADC中,
AC=6,AD=4
,
cos∠CAD=
=
=
,
则∠CAD=30°,
∵AD为∠BAC的平分线,
∴∠CAB=60°,
在Rt△ABC中,
=tan60°,
∴BC=6
,
=cos60°,
=
,
AB=12,
∠B=90°-60°=30°.
 解:在Rt△ADC中,
解:在Rt△ADC中,AC=6,AD=4
| 3 |
cos∠CAD=
| AC |
| AD |
| 6 | ||
4
|
| ||
| 2 |
则∠CAD=30°,
∵AD为∠BAC的平分线,
∴∠CAB=60°,
在Rt△ABC中,
| BC |
| 6 |
∴BC=6
| 3 |
| AC |
| AB |
| 6 |
| AB |
| 1 |
| 2 |
AB=12,
∠B=90°-60°=30°.
点评:本题考查了解直角三角形,利用三角函数在各直角三角形中解答,要充分利用好特殊角的三角函数值.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
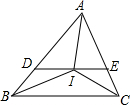 如图,△ABC中,IB,IC分别平分∠ABC,∠ACB,过I点作DE∥BC,分别交AB于D,交AC于E,给出下列结论:
如图,△ABC中,IB,IC分别平分∠ABC,∠ACB,过I点作DE∥BC,分别交AB于D,交AC于E,给出下列结论:①△DBI是等腰三角形;②△ACI是等腰三角形;③AI平分∠BAC;④△ADE周长等于AB+AC,
其中正确的是( )
| A、①②③ | B、②③④ |
| C、①③④ | D、①②④ |
元旦节日期间,某商场为了促销,每件夹克按成本价提高50%后标价,后因季节关系按标价的8折出售,每件以168元卖出,这批夹克每件的成本价是( )
| A、80元 | B、84元 |
| C、140元 | D、100元 |
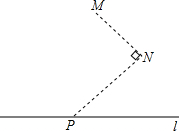 如图所示,在水渠l的同一侧有两个水池M与N,把水渠水先引到水池N,再由N引人水池M.连接MN,作∠MNP=90°,NP交l于点P,将水渠水由P放到N,再由N放到M,所行路径最短,对吗?如果不对,你是怎样设计的?写出你的设计方案.
如图所示,在水渠l的同一侧有两个水池M与N,把水渠水先引到水池N,再由N引人水池M.连接MN,作∠MNP=90°,NP交l于点P,将水渠水由P放到N,再由N放到M,所行路径最短,对吗?如果不对,你是怎样设计的?写出你的设计方案. 如图,在平面直角坐标中,矩形OABC的顶点O为坐标原点,OA在x轴上,OC在y轴上,点B的坐标为(-3,4),反比例函数
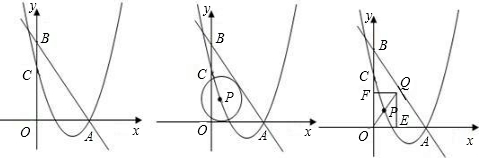
如图,在平面直角坐标中,矩形OABC的顶点O为坐标原点,OA在x轴上,OC在y轴上,点B的坐标为(-3,4),反比例函数 如图,已知一次函数y1=x-6与反比例函数y2=
如图,已知一次函数y1=x-6与反比例函数y2=