题目内容
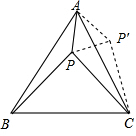 如图,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=
如图,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=考点:旋转的性质,全等三角形的判定与性质,等边三角形的性质
专题:
分析:此类题要充分运用旋转的性质,以及全等三角形的性质得对应角相等,对应边相等,得出∠PAP′=60°,再利用等边三角形的判定得出△APP′为等边三角形,即可得出∠APP′的度数,即可得出答案.
解答:解:将△ABP绕顶点A旋转到△ACP′处,
∴△BAP≌△CAP′,
∴AB=AC,AP=AP′,∠BAP=∠CAP′,
∴∠BAC=∠PAP′=60°,
∴△APP′是等边三角形,
∴∠APP′=60°,
∴P′C=PB=4,PP′=PA=3,P′C=PC=5,
∴∠PP′C=90°,
∴△PP′C是直角三角形,
∴∠APB=∠AP′C=∠APP′+∠P′PC=60°+90°=150°,
∴∠BPA=150°;
故答案是:150°,△ABP;

∴△BAP≌△CAP′,
∴AB=AC,AP=AP′,∠BAP=∠CAP′,
∴∠BAC=∠PAP′=60°,
∴△APP′是等边三角形,
∴∠APP′=60°,
∴P′C=PB=4,PP′=PA=3,P′C=PC=5,
∴∠PP′C=90°,
∴△PP′C是直角三角形,
∴∠APB=∠AP′C=∠APP′+∠P′PC=60°+90°=150°,
∴∠BPA=150°;
故答案是:150°,△ABP;
点评:此题主要考查了旋转的性质,充分运用全等三角形的性质找到相关的角和线段之间的关系是解题关键.

练习册系列答案
相关题目
 如图,已知一次函数y1=x-6与反比例函数y2=
如图,已知一次函数y1=x-6与反比例函数y2=
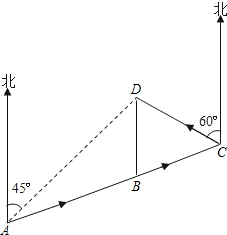 如图,要环绕A、B、C、D四地修筑一条高等级公路ABCDA.已知A、B、C三地在同一直线上,D地在A地的北偏东45°方向,在B地的正北方向,在C地北偏西60°方向,C地在A地的北偏东75°方向,B、D两地相距10km.如果该公路每公里造价为2000万元,求该公路全长的造价是多少万元?(用根号表示)
如图,要环绕A、B、C、D四地修筑一条高等级公路ABCDA.已知A、B、C三地在同一直线上,D地在A地的北偏东45°方向,在B地的正北方向,在C地北偏西60°方向,C地在A地的北偏东75°方向,B、D两地相距10km.如果该公路每公里造价为2000万元,求该公路全长的造价是多少万元?(用根号表示)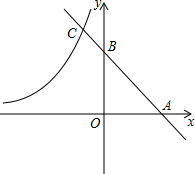 如图,直线y=-x+m与双曲线y=-
如图,直线y=-x+m与双曲线y=-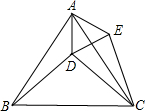 如图,D是等边△ABC内的一点,以AD为边向外作等边△ADE.
如图,D是等边△ABC内的一点,以AD为边向外作等边△ADE.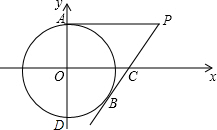 如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,D点P(2
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,D点P(2