题目内容
14.如果我们定义f(x)=$\frac{x}{1+x}$,(例如:f(5)=$\frac{5}{1+5}$=$\frac{5}{6}$),试计算下面算式的值:f($\frac{1}{2015}$)+…f($\frac{1}{2}$)+f($\frac{1}{1}$)+f(0)+f(1)+f(2)+…+f(2015)=2015.
分析 根据题意得出规律f(x)+f($\frac{1}{x}$)=1,原式结合后计算即可得到结果.
解答 解:f(x)+f($\frac{1}{x}$)=$\frac{x}{1+x}$+$\frac{\frac{1}{x}}{1+\frac{1}{x}}$=$\frac{x+1}{x+1}$=1,
则原式=[f($\frac{1}{2015}$)+f(2015)]+…+[f($\frac{1}{2}$)+f(2)]+[f($\frac{1}{1}$)+f(1)]+f(0)=2015,
故答案为:2015.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
5.九年级数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤70且x为整数)天的售价目与销量的相关信息如下表:
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于3250元?请直接写出结果.
| 时间x(天) | 1≤x≤40 | 40≤x≤70 |
| 售价(元/件) | x+45 | 85 |
| 每天销售(件) | 150-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于3250元?请直接写出结果.
2.某手机专卖店销售A,B两种型号的手机,如表是近两周的销售情况:
(1)求每台A型手机和B型手机的销售利润;
(2)该手机专卖店计划一次购进两种型号的手机共100台,其中A型号手机的进货量不超过B型号手机进货量的2倍.设购进A型号手机x台,这100台手机的销售总利润为y元.
①求y关于x的函数表达式;
②该商店购进A型号和B型号手机各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型号手机的出厂价提高a(0<a<100)元,对B型号手机的出厂价下降a(0<a<100)元,且限定该手机专卖店至少购进A型号手机20台.若该手机专卖店保持两种手机的售价不变,请根据以上信息及(2)中条件,设计出使这100台手机销售总利润最大的进货方案.
| 销售时段 | 销售数量 | 销售利润 | |
| A型 | B型 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第二周 | 4台 | 10台 | 3000元 |
(2)该手机专卖店计划一次购进两种型号的手机共100台,其中A型号手机的进货量不超过B型号手机进货量的2倍.设购进A型号手机x台,这100台手机的销售总利润为y元.
①求y关于x的函数表达式;
②该商店购进A型号和B型号手机各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型号手机的出厂价提高a(0<a<100)元,对B型号手机的出厂价下降a(0<a<100)元,且限定该手机专卖店至少购进A型号手机20台.若该手机专卖店保持两种手机的售价不变,请根据以上信息及(2)中条件,设计出使这100台手机销售总利润最大的进货方案.
4.用配方法解下列方程时,配方正确的是( )
| A. | 方程x2-6x-5=0,可化为(x-3)2=4 | |
| B. | 方程y2-2y-2015=0,可化为(y-1)2=2015 | |
| C. | 方程a2+8a+9=0,可化为(a+4)2=25 | |
| D. | 方程2x2-6x-7=0,可化为${({x-\frac{3}{2}})^2}=\frac{23}{4}$ |
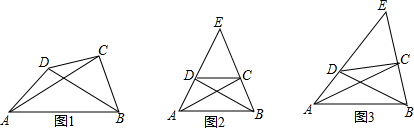
 如图,AC与BD相交于点O,且AB=CD,请添加一个条件∠A=∠C,使得△ABO≌△CDO.
如图,AC与BD相交于点O,且AB=CD,请添加一个条件∠A=∠C,使得△ABO≌△CDO.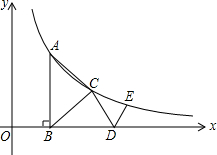 如图,△ABC是等腰直角三角形,斜边AD⊥x轴于D,顶点A,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,再作等腰Rt△CDE,使直角顶点E在该函数图象上,顶点D在x轴的正半轴上,则点E的坐标是($\sqrt{3}$+1,$\sqrt{3}$-1).
如图,△ABC是等腰直角三角形,斜边AD⊥x轴于D,顶点A,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,再作等腰Rt△CDE,使直角顶点E在该函数图象上,顶点D在x轴的正半轴上,则点E的坐标是($\sqrt{3}$+1,$\sqrt{3}$-1).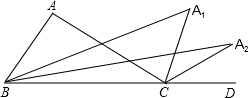 如图,在△ABC,∠BAC=100°,延长BC到D,∠ABC与∠ACD的角平分线相交于A1,若∠A1BC与∠A1CD的角平分线相交于点A2,以此类推,∠An-1BC与∠An-1CD的角平分线相交于点An,则∠An=$\frac{100°}{{2}^{n}}$.
如图,在△ABC,∠BAC=100°,延长BC到D,∠ABC与∠ACD的角平分线相交于A1,若∠A1BC与∠A1CD的角平分线相交于点A2,以此类推,∠An-1BC与∠An-1CD的角平分线相交于点An,则∠An=$\frac{100°}{{2}^{n}}$.