题目内容
5.九年级数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤70且x为整数)天的售价目与销量的相关信息如下表:| 时间x(天) | 1≤x≤40 | 40≤x≤70 |
| 售价(元/件) | x+45 | 85 |
| 每天销售(件) | 150-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于3250元?请直接写出结果.
分析 (1)根据单价乘以数量,可得利润,可得答案;
(2)根据分段函数的性质,可分别得出最大值,根据有理数的比较,可得答案;
(3)根据二次函数值大于或等于3250,一次函数值大于或等于3250,可得不等式,根据解不等式组,可得答案.
解答 解:(1)当1≤x<40时,y=(150-2x)(x+45-30)=-2x2+120x+2250,
当40≤x≤70时,y=(150-2x)(85-30)=-110x+8250,
综上所述:y=$\left\{\begin{array}{l}{-2{x}^{2}+120x+2250(1≤x<40)}\\{-110x+8250(40≤x≤70)}\end{array}\right.$;
(2)当1≤x<40时,二次函数开口向下,二次函数对称轴为x=30,
当x=30时,y最大=-2×302+120×30+2250=4050,
当40≤x≤70时,y随x的增大而减小,
当x=40时,y最大=3850,
综上所述,该商品第30天时,当天销售利润最大,最大利润是4050元;
(3)当1≤x<40时,y=-2x2+120x+2250≥3250,解得10≤x≤50,
因此利润不低于3250元的天数是10≤x<40,共30天;
当40≤x≤70时,y=-110x+8250≥3250,解得x≤45$\frac{5}{11}$,
因此利润不低于3250元的天数是40≤x≤45,共6天,
所以该商品在销售过程中,共36天每天销售利润不低于3250元.
点评 本题考查了二次函数的应用,利用单价乘以数量求函数解析式,利用了函数的性质求最值.

练习册系列答案
相关题目
10.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{36}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{a+4}$ |
10.某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部注满;当每个房间每天的定价增加10元时,就会有一个房间空闲,如果游客居住房间,宾客需对每个房间每天支出20元的各种费用,当房价定位多少元时,宾客利润最大,最大利润是多少?设每个房间定价增加10x元,宾馆每天的利润为y元.
(Ⅰ)分析:根据问题中的数量关系,用含x的式子填表:
(Ⅱ)由以上分析,用含x的式子表示y,并求出问题的解.
(Ⅰ)分析:根据问题中的数量关系,用含x的式子填表:
| 原价 | 每个房间增加10元 | 每个房间增加20元 | … | 每个房间增加10x元 | |
| 每个房价定价 | 180 | 190 | 200 | … | |
| 房住房间数量 | 50 | 49 | 48 | … |
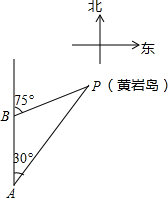 如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:$\sqrt{2}$≈1.414,结果精确到0.1)
如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:$\sqrt{2}$≈1.414,结果精确到0.1)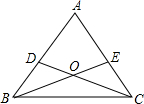 如图,已知△ABC中,AB=AC,点D、E分别在AB、AC上,且BD=CE.
如图,已知△ABC中,AB=AC,点D、E分别在AB、AC上,且BD=CE.