题目内容
2.某手机专卖店销售A,B两种型号的手机,如表是近两周的销售情况:| 销售时段 | 销售数量 | 销售利润 | |
| A型 | B型 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第二周 | 4台 | 10台 | 3000元 |
(2)该手机专卖店计划一次购进两种型号的手机共100台,其中A型号手机的进货量不超过B型号手机进货量的2倍.设购进A型号手机x台,这100台手机的销售总利润为y元.
①求y关于x的函数表达式;
②该商店购进A型号和B型号手机各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型号手机的出厂价提高a(0<a<100)元,对B型号手机的出厂价下降a(0<a<100)元,且限定该手机专卖店至少购进A型号手机20台.若该手机专卖店保持两种手机的售价不变,请根据以上信息及(2)中条件,设计出使这100台手机销售总利润最大的进货方案.
分析 (1)设每台A型手机利润为a元,每台B型手机的销售利润为b元;根据题意列出方程组求解,
(2)①据题意得,y=300x+180(100-x);②利用不等式求出x的范围,又因为y=120x+18000是增函数,即可得出答案;
(3)据题意得,y=(300-a)x+(180+a)(100-x),即y=(120-2a)x+18000+100a,分三种情况讨论,①当0<a<60时,120-2a>0,y随x的增大而增大,②a=60时,120-2a=0,y=24000,③当60<a<100时,120-2a<0,y随x的增大而减小,分别进行求解.
解答 解:(1)设每台A型手机销售利润为a元,每台B型手机的销售利润为b元;根据题意得:
$\left\{\begin{array}{l}{3a+5b=1800}\\{4a+10b=3000}\end{array}\right.$,
解得:
$\left\{\begin{array}{l}{a=300}\\{b=180}\end{array}\right.$,
答:每台A型手机销售利润为100元,每台B型手机的销售利润为150元.
(2)①据题意得,y=y=300x+180(100-x)=120x+18000;
②据题意得,x≤2(100-x),解得x≤66$\frac{2}{3}$,
∵y=120x+18000,120>0,
∴y随x的增大而增大,
∵x为正整数,
∴当x=66时,y取最大值,则100-66=34,
即商店购进66台A型手机和34台B型手机的销售利润最大.
(3)据题意得,y=(300-a)x+(180+a)(100-x),即y=(120-2a)x+18000+100a,20≤x≤66$\frac{2}{3}$,
①当0<a<60时,120-2a>0,y随x的增大而增大
∴当x=66时,y取最大值,
②a=60时,120-2a=0,y=18000+100a=24000,
即商店购进A型手机数量满足x≤66$\frac{2}{3}$,的整数时,均获得最大利润;
③当60<a<100时,120-2a<0,y随x的增大而减小,
∴当x=20时,y取得最大值.
即商店购进20台A型手机和80台B型手机的销售利润最大.
点评 本题主要考查了一次函数的应用,二元一次方程组及一元一次不等式的应用,解题的关键是根据一次函数x值的增大而确定y值的增减情况.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | $\sqrt{24}$ | B. | $\sqrt{36}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{a+4}$ |
(Ⅰ)分析:根据问题中的数量关系,用含x的式子填表:
| 原价 | 每个房间增加10元 | 每个房间增加20元 | … | 每个房间增加10x元 | |
| 每个房价定价 | 180 | 190 | 200 | … | |
| 房住房间数量 | 50 | 49 | 48 | … |
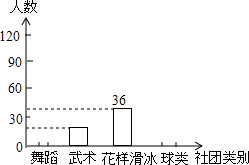 某校开展第二课堂活动,准备组建舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球)、花样滑冰四类社团、为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校开展第二课堂活动,准备组建舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球)、花样滑冰四类社团、为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:“你最喜爱的社团”调查统计图表
| 社团类别 | 人数 | 占总人数的比例 |
| 舞蹈 | b | 25% |
| 武术 | 24 | 10% |
| 花样滑冰 | 36 | n% |
| 球类 | a | 50% |
(2)补全表格和统计图:a=120;b=60,n=15;
(3)被调查喜爱球类的学生中有12人最喜爱乒乓球,若该校有2600名学生,请估计该校最喜爱乒乓球的人数.
 如图,五边形ABCDE中,AB=AE,BC=ED,O为CD的中点,连接BO,EO,BO=EO,试探索AO与CD的位置关系.
如图,五边形ABCDE中,AB=AE,BC=ED,O为CD的中点,连接BO,EO,BO=EO,试探索AO与CD的位置关系. 已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C、A(-1,1),B(-3,1)动点P从点O出发,沿着x轴负方向以每秒2个单位长度的速度移动,过点P作PQ垂直与直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2)
已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C、A(-1,1),B(-3,1)动点P从点O出发,沿着x轴负方向以每秒2个单位长度的速度移动,过点P作PQ垂直与直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2)